
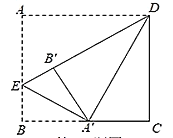
°æƒø°ø»ÁÕº1£¨‘⁄°˜ABC÷–£¨AC£ΩnAB£¨°œCAB£Ω¶¡£¨µ„E£¨F∑÷±‘⁄AB£¨AC…œ«“EF°ŒBC£¨∞—°˜AEF»∆µ„AÀ≥ ±’Ζ˝◊™µΩ»ÁÕº2µƒŒª÷√£Æ¡¨Ω”CF£¨BE£Æ

£®1£©«Û÷§£∫°œACF£Ω°œABE£ª
£®2£©»Ùµ„M£¨N∑÷± «EF£¨BCµƒ÷–µ„£¨µ±¶¡£Ω90°„ ±£¨«Û÷§£∫BE2+CF2£Ω4MN2£ª
£®3£©»ÁÕº3£¨µ„M£¨N∑÷±‘⁄EF£¨BC…œ«“![]() £Ω
£Ω![]() £Ω
£Ω![]() £¨»Ùn£Ω
£¨»Ùn£Ω![]() £¨¶¡£Ω135°„£¨BE£Ω
£¨¶¡£Ω135°„£¨BE£Ω![]() £¨÷±Ω”–¥≥ˆMNµƒ≥§£Æ
£¨÷±Ω”–¥≥ˆMNµƒ≥§£Æ
°æ¥∞∏°ø£®1£©º˚Ω‚Œˆ£ª£®2£©º˚Ω‚Œˆ£ª£®3£©![]()
°æΩ‚Œˆ°ø
£®1£©÷§√˜°˜CAF°◊°˜BAEº¥ø…Ω‚æˆŒ £ª
£®2£©—”≥§BEΩªCFµƒ—”≥§œþ”⁄H£¨¡¨Ω”BF£¨»°BFµƒ÷–µ„J£¨¡¨Ω”NJ£¨JM£¨…ËACΩªBH”⁄µ„O£Æ ◊œ»÷§√˜CF°ÕBE£¨¿˚”√»˝Ω«–Œµƒ÷–Œªœþ∂®¿Ì÷§√˜°˜NJM «÷±Ω«»˝Ω«–Œ£¨¿˚”√π¥π…∂®¿Ìº¥ø…Ω‚æˆŒ £Æ
£®3£©»ÁÕº3÷–£¨—”≥§BEΩªCFµƒ—”≥§œþ”⁄H£¨¡¨Ω”BF£¨‘⁄FB…œ»°“ªµ„J£¨ πµ√FJ£∫JB£Ω1£∫2£¨¡¨Ω”NJ£¨JM£Æ÷§√˜°œMJN£Ω45°„£¨NJ£Ω![]() £¨MJ£Ω
£¨MJ£Ω![]() £¨»ÁÕº4÷–£¨‘⁄°˜NJM÷–£¨◊˜MK°ÕNJ”⁄K£¨Ω‚÷±Ω«»˝Ω«–Œ«Û≥ˆMNº¥ø…£Æ
£¨»ÁÕº4÷–£¨‘⁄°˜NJM÷–£¨◊˜MK°ÕNJ”⁄K£¨Ω‚÷±Ω«»˝Ω«–Œ«Û≥ˆMNº¥ø…£Æ
£®1£©÷§√˜£∫
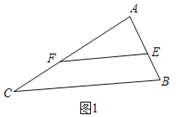
‘⁄»ÁÕº1÷–£¨
°þEF°ŒBC£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
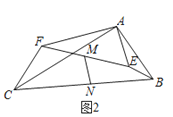
»ÁÕº2÷–£¨
°þ°œCAB£Ω°œEAF£¨
°ý°œCAF£Ω°œBAE£¨
°þ![]() £¨
£¨
°ý°˜CAF°◊°˜BAE£¨
°ý°œACF£Ω°œABE£Æ
£®2£©÷§√˜£∫‘⁄Õº2÷–£¨—”≥§BEΩªCFµƒ—”≥§œþ”⁄H£¨¡¨Ω”BF£¨»°BFµƒ÷–µ„J£¨¡¨Ω”NJ£¨JM£¨…ËACΩªBH”⁄µ„O£Æ
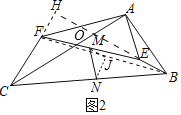
°þ°œOCH£Ω°œOBA£¨°œCOH£Ω°œBOA£¨
°ý°œH£Ω°œOAB£Ω90°„£¨
°ýCF°ÕBE£¨
°þCN£ΩBN£¨FJ£ΩJB£¨
°ýJN°ŒCF£¨JN£Ω![]() CF£¨
CF£¨
°þFM£ΩME£¨FJ£ΩJB£¨
°ýMJ°ŒBE£¨MJ£Ω![]() BE£¨
BE£¨
°þCF°ÕBE£¨
°ýNJ°ÕJM£¨
°ý°œNJM£Ω90°„£¨
°ýJN2+JM2£ΩMN2£¨
°ý£®![]() CF£©2+£®
CF£©2+£®![]() BE£©2£ΩMN2£¨
BE£©2£ΩMN2£¨
°ýBE2+CF2£Ω4MN2£Æ
£®3£©Ω‚£∫‘⁄Õº3÷–£¨—”≥§BEΩªCFµƒ—”≥§œþ”⁄H£¨¡¨Ω”BF£¨‘⁄FB…œ»°“ªµ„J£¨ πµ√FJ£∫JB£Ω1£∫2£¨¡¨Ω”NJ£¨JM£Æ
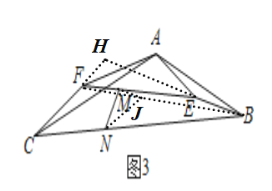
Õ¨∑®ø…÷§°œH£Ω°œCAB£Ω135°„£¨
°þCN£∫BN£ΩFJ£∫JB£Ω1£∫2£¨
°ýNJ°ŒCF£¨NJ£Ω![]() CF£¨
CF£¨
°þFM£∫ME£ΩFJ£∫JB£Ω1£∫2£¨
°ýMJ°ŒBE£¨MJ£Ω![]() BE£¨
BE£¨
°ý°˜MJN÷–°œMJNµƒÕ‚Ω«Œ™135°„£¨
°ý°œMJN£Ω45°„£¨
”…“‚BE£Ω![]() £¨CF£Ω2£¨
£¨CF£Ω2£¨
°ýNJ£Ω![]() £¨MJ£Ω
£¨MJ£Ω![]() £¨
£¨
»ÁÕº4÷–£¨‘⁄°˜NJM÷–£¨◊˜MK°ÕNJ”⁄K£Æ
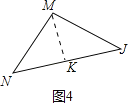
°þ°œJ£Ω°œJMK£Ω45°„£¨MJ£Ω![]() £¨
£¨
°ýMK£ΩKJ£Ω![]() £¨
£¨
°ýNK£ΩNJ©ÅKJ£Ω1£¨
°ýMN£Ω![]() =
=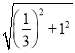 £Ω
£Ω![]() £Æ
£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™∆Ω––Àƒ±þ–Œ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() .∆Ω––Àƒ±þ–Œ
.∆Ω––Àƒ±þ–Œ![]() µƒ∂•µ„
µƒ∂•µ„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ£®µ„
…œ£®µ„![]() ‘⁄
‘⁄![]() µƒ◊Û±þ£©£¨∂•µ„
µƒ◊Û±þ£©£¨∂•µ„![]() ∑÷±‘⁄œþ∂Œ
∑÷±‘⁄œþ∂Œ![]() ∫Õ
∫Õ![]() …œ.
…œ.
£®1£©«Û÷§£∫![]() £ª
£ª
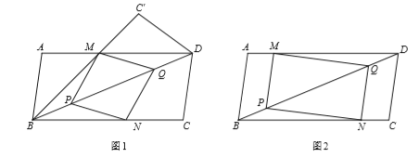
£®2£©»ÁÕº1£¨Ω´![]() —ÿ÷±œþ
—ÿ÷±œþ![]() ’€µ˛µ√µΩ
’€µ˛µ√µΩ![]() £¨µ±
£¨µ±![]() «°∫√æ≠π˝µ„
«°∫√æ≠π˝µ„![]() ±£¨«Û÷§£∫Àƒ±þ–Œ
±£¨«Û÷§£∫Àƒ±þ–Œ![]() «¡‚–Œ£ª
«¡‚–Œ£ª
£®3£©»ÁÕº2£¨»ÙÀƒ±þ–Œ![]() «æÿ–Œ£¨«“
«æÿ–Œ£¨«“![]() £¨«Û
£¨«Û![]() µƒ≥§.£®Ω·π˚÷–µƒ∑÷ƒ∏ø…±£¡Ù∏˘ Ω£©
µƒ≥§.£®Ω·π˚÷–µƒ∑÷ƒ∏ø…±£¡Ù∏˘ Ω£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
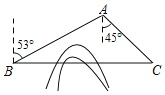
°æƒø°ø»ÁÕº£¨Cµÿ‘⁄Bµÿµƒ’˝∂´∑ΩœÚ£¨“Ú”–¥Û…Ω◊Ë∏Ù£¨”…BµÿµΩCµÿ–Ë»∆––Aµÿ£¨“—÷™AµÿŒª”⁄Bµÿ±±∆´∂´53°„∑ΩœÚ£¨æý¿ÎBµÿ516«ß√◊£¨CµÿŒª”⁄Aµÿƒœ∆´∂´45°„∑ΩœÚ£Æœ÷¥ÚÀ„¥ÚÕ®¥©…ΩÀ̵¿£¨Ω®≥…¡Ωµÿ÷±¥Ô∏þÃ˙£¨«ÛΩ®≥…∏þÃ˙∫Û¥”Bµÿ«∞Õ˘Cµÿµƒ¬∑≥ãƣ®Ω·π˚æ´»∑µΩ1«ß√◊£©£®≤Œøº ˝æð£∫sin53°„£Ω![]() £¨cos53°„£Ω
£¨cos53°„£Ω![]() £¨tan53°„£Ω
£¨tan53°„£Ω![]() £©
£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
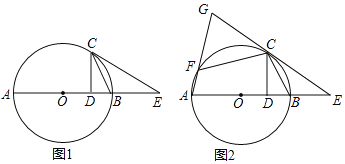
°æƒø°ø»ÁÕº1£¨ABŒ™°—Oµƒ÷±æ∂£¨CŒ™°—O…œ“ªµ„£¨¡¨Ω”CB£¨π˝C◊˜CD°ÕAB”⁄µ„D£¨π˝µ„C◊˜°œBCE£¨ π°œBCE£Ω°œBCD£¨∆‰÷–CEΩªABµƒ—”≥§œþ”⁄µ„E£Æ
£®1£©«Û÷§£∫CE «°—Oµƒ«–œþ£Æ
£®2£©»ÁÕº2£¨µ„F‘⁄°—O…œ£¨«“¬˙◊„°œFCE£Ω2°œABC£¨¡¨Ω”AFæÆ—”≥§ΩªECµƒ—”≥§œþ”⁄µ„G£Æ
¢Ÿ ‘ÃΩæøœþ∂ŒCF”ÎCD÷ƺ‰¬˙◊„µƒ ˝¡øπÿœµ£ª
¢⁄»ÙCD£Ω4£¨BD£Ω2£¨«Ûœþ∂ŒFGµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨AB «°—Oµƒ÷±æ∂£¨C «°—0…œµƒ“ªµ„£¨÷±œþMNæ≠π˝µ„C£¨π˝µ„A◊˜÷±œþMNµƒ¥πœþ£¨¥π◊„Œ™µ„D£¨«“°œBAC=°œDAC
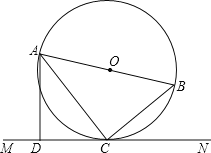
£®1£©≤¬œÎ÷±œþMN”ΰ—OµƒŒª÷√πÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
£®2£©»ÙCD=6£¨cos°œACD=![]() £¨«Û°—Oµƒ∞Îæ∂£Æ
£¨«Û°—Oµƒ∞Îæ∂£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
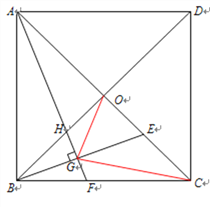
°æƒø°ø»ÁÕº£¨‘⁄’˝∑Ω–ŒABCD÷–£¨∂‘Ω«œþAC°¢BDœýΩª”⁄µ„O£¨EŒ™OC…œ∂ص„(”ε„O≤ª÷ÿ∫œ)£¨◊˜AF°ÕBE£¨¥π◊„Œ™G£¨ΩªBC”⁄F£¨ΩªB0”⁄H£¨¡¨Ω”OG£¨CC£Æ
(1)«Û÷§£∫AH=BE£ª
(2) ‘ÃΩæø£∫°œAGOµƒ∂» ˝ «∑ÒŒ™∂®÷µ?«ÎÀµ√˜¿Ì”…£ª
(3)»ÙOG°ÕCG£¨BG=![]() £¨«Û°˜OGCµƒ√ʪ˝£Æ
£¨«Û°˜OGCµƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™AB «°—Oµƒ÷±æ∂£¨œ“CD°ÕAB”⁄H£¨π˝CD—”≥§œþ…œ“ªµ„E◊˜°—Oµƒ«–œþΩªABµƒ—”≥§œþ”⁄F£¨«–µ„Œ™G£¨¡¨Ω”AGΩªCD”⁄K£Æ
£®1£©»ÁÕº1£¨«Û÷§£∫KE=GE£ª
£®2£©»ÁÕº2£¨¡¨Ω”CABG£¨»Ù°œFGB=![]() °œACH£¨«Û÷§£∫CA°ŒFE£ª
°œACH£¨«Û÷§£∫CA°ŒFE£ª
£®3£©»ÁÕº3£¨‘⁄£®2£©µƒÃıº˛œ¬£¨¡¨Ω”CGΩªAB”⁄µ„N£¨»ÙsinE=![]() £¨AK=
£¨AK=![]() £¨«ÛCNµƒ≥§£Æ
£¨«ÛCNµƒ≥§£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
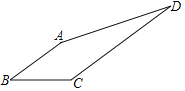
°æƒø°ø»ÁÕº£¨‘⁄Àƒ±þ–ŒABCD÷–£¨AB°ŒCD£¨2AB=2BC=CD=10£¨tanB=![]() £¨‘ÚAD=______£Æ
£¨‘ÚAD=______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄æÿ–Œ![]() ÷–£¨
÷–£¨![]() £ÆΩ´
£ÆΩ´![]() œÚƒ⁄∑≠’€£¨µ„
œÚƒ⁄∑≠’€£¨µ„ ![]() ¬‰‘⁄
¬‰‘⁄![]() …œ£¨º«Œ™
…œ£¨º«Œ™![]() £¨’€∫€Œ™
£¨’€∫€Œ™![]() £Æ»ÙΩ´
£Æ»ÙΩ´![]() —ÿ
—ÿ![]() œÚƒ⁄∑≠’€£¨µ„
œÚƒ⁄∑≠’€£¨µ„![]() «°∫√ ¬‰‘⁄
«°∫√ ¬‰‘⁄![]() …œ£¨º«Œ™
…œ£¨º«Œ™![]() £¨‘Ú
£¨‘Ú![]() µƒ≥§Œ™£® £©
µƒ≥§Œ™£® £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com