
【题目】如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD、AE,则∠EAD的度数为( )
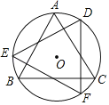
A.150°B.135°C.120°D.105°
【答案】C
【解析】
连结OA、OE、OD、AE、AD,根据旋转的性质得∠AOD=30°,再根据圆周角定理得∠AED=![]() ∠AOD=15°,然后根据等边三角形的性质得∠EFD=60°,则∠DOE=120°,求出∠AOE=∠DOE-∠AOD=90°,则∠ADE=45°,根据三角形内角和可求出∠EAD的度数.
∠AOD=15°,然后根据等边三角形的性质得∠EFD=60°,则∠DOE=120°,求出∠AOE=∠DOE-∠AOD=90°,则∠ADE=45°,根据三角形内角和可求出∠EAD的度数.
如图,连结OA、OE、OD、AE、AD,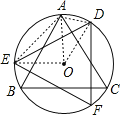
∵△ABC绕点O顺时针旋转30°得到△DEF,
∴∠AOD=30°,
∴∠AED=![]() ∠AOD=15°,
∠AOD=15°,
∵△DEF为等边三角形,
∴∠EFD=60°,
∴∠DOE=2∠EFD=120°,
∴∠AOE=∠DOE-∠AOD=120°-30°=90°,
∴∠ADE=![]() ∠AOE=45°,
∠AOE=45°,
∴∠EAD=180°-∠AED-∠ADE=180°-15°-45°=120°.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙0上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC
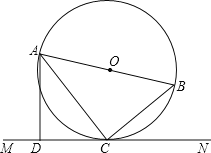
(1)猜想直线MN与⊙O的位置关系,并说明理由;
(2)若CD=6,cos∠ACD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线BC与⊙A相切于点C,过B作CB的垂线交⊙O于D,E两点,已知AC=![]() ,CB=a,则以BE,BD的长为两根的一元二次方程是( )
,CB=a,则以BE,BD的长为两根的一元二次方程是( )
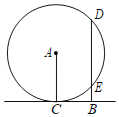
A.x2+bx+a2=0B.x2﹣bx+a2=0C.x2+bx﹣a2=0D.x2﹣bx﹣a2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与x轴、y轴分别交于点A、B,抛物线
与x轴、y轴分别交于点A、B,抛物线![]() 经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则
经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则![]() 的取值范围是____.
的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·荆门中考)如图,天星山山脚下西端A处与东端B处相距800(1+![]() )米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为
)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为![]() 米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商贸公司以每千克![]() 元的价格购进一种干果,计划以每千克
元的价格购进一种干果,计划以每千克![]() 元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量
元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量![]() (千克)与每千克降价
(千克)与每千克降价![]() (元)
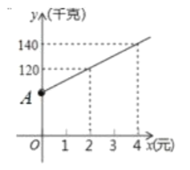
(元)![]() 之间满足一次函数关系,其图象如图所示: .
之间满足一次函数关系,其图象如图所示: .
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)函数图象中点![]() 表示的实际意义是 ;
表示的实际意义是 ;
(3)该商贸公司要想获利![]() 元,则这种干果每千克应降价多少元?
元,则这种干果每千克应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 分别与
分别与![]() ,
,![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 上,抛物线
上,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于另一点
轴交于另一点![]() .
.
(1)求点![]() 的坐标(用只含
的坐标(用只含![]() ,
,![]() 的代数式表示);
的代数式表示);
(2)当![]() 时,若点
时,若点![]() ,
,![]() 均在抛物线
均在抛物线![]() 上,且
上,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 有最小值
有最小值![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
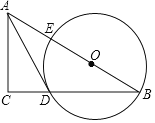
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B,
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O 的半径.
,求⊙O 的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com