
【题目】直线![]() 与x轴、y轴分别交于点A、B,抛物线
与x轴、y轴分别交于点A、B,抛物线![]() 经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则
经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则![]() 的取值范围是____.
的取值范围是____.
【答案】![]() 或
或![]() 或
或![]() .
.
【解析】
根据坐标轴上点的坐标特征可求点A,B的坐标,根据平移的性质可求点C的坐标,结合图形,分三种情况:①a>0;②a<0,③抛物线的顶点在线段BC上;进行讨论即可求解.
解:与x轴交点:令y=0代入直线y=4x+4得x=-1,
∴A(-1,0),
与y轴交点:令x=0代入直线y=4x+4得y=4,
∴B(0,4),
∵点B向右平移5个单位长度,得到点C,
∴C(5,4)
将点A(-1,0)代入抛物线![]() 中得
中得![]() ,即
,即![]()
∴抛物线的对称轴![]()
由抛物线的对称性可知抛物线也一定过A的对称点(3,0),
①a>0时,如图1,将x=0代入抛物线得![]() ,
,
∵抛物线与线段BC恰有一个公共点,
∴![]() ,
,
∴![]()
将![]() 代入抛物线得
代入抛物线得![]() ,
,
∴![]() ,
,
∴![]() ;
;
②a<0时,如图2,
将x=0代入抛物线得![]() ,
,
∵抛物线与线段BC恰有一个公共点,
∴![]() ,
,
∴![]() ;
;
③当抛物线的顶点在线段BC上时,则顶点为(1,4),如图3,
将点(1,4)代入抛物线得![]() ,
,
解得![]() .
.
综上所述,![]() 或
或![]() 或
或![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图所示,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,沿射线
同时出发,沿射线![]() 、线段
、线段![]() 向点
向点![]() 的方向运动(点
的方向运动(点![]() 可运动到
可运动到![]() 的延长线上),当动点
的延长线上),当动点![]() 运动到点
运动到点![]() 时,
时,![]() 、
、![]() 两点同时停止运动.联结
两点同时停止运动.联结![]() 、
、![]() 、
、![]() ,过
,过![]() 三边的中点作
三边的中点作![]() .设动点
.设动点![]() 、
、![]() 的速度都是1个单位/秒,
的速度都是1个单位/秒,![]() 、
、![]() 运动的时间为
运动的时间为![]() 秒.试解答下列问题:
秒.试解答下列问题:
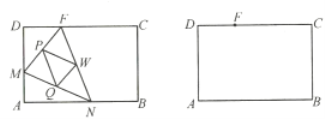
(1)说明![]() ;
;
(2)设![]() ,试问
,试问![]() 为何值时,
为何值时,![]() 为直角三角形?
为直角三角形?
(3)试用含![]() 的代数式表示
的代数式表示![]() ,并求当
,并求当![]() 为何值时,
为何值时,![]() 最小?求此时
最小?求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两家公司员工日工资情况:甲公司日工资是底薪100元,每完成一件产品工资计3元;乙公司无底薪,40件以内(含40件)产品的部分每件产品工资计8元,超出40件的部分每件产品工资计10元,为此,在这两家公司各随机调查了100名工人日完成产品数,并整理得到如下频数分布表:
日完成产品数 | 38 | 39 | 40 | 41 | 42 |
甲公司工人数 | 20 | 40 | 20 | 10 | 10 |
乙公司工人数 | 10 | 20 | 20 | 40 | 10 |
(1)若甲、乙公司日工资加上其他福利,总的待遇相同,A、B两人分别到甲、乙公司应聘,都选中甲公司的概率是多少?
(2)试以这两家公司各100名工人日工资的平均数作为决策依据,若某人要去这两家公司应聘,为他做出选择,去哪一家公司的经济收入可能会多一些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣4,﹣2),B(﹣2,﹣2),C(﹣1,0).

(1)将△ABC向右平移5个单位长度,画出平移后的△A1B1C1;
(2)将△ABC绕点C旋转180°,画出旋转后的△A2B2C,并直接写出点A运动的路径长;
(3)请直接写出△B1C1B2的外心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果超市以每千克6元的价格购进了一批水果,经测算,此水果超市每天需支出固定费用(包括房租,水电费,员工工资等)为600元.若该种水果的销售单价不超过10元,则日销售量为300千克;若该种水果的销售单价超过10元,则每超过1元,日销售就减少12千克.设该种水果的销售单价为x(x>6,且x为整数)元,日净收入为y元(日净收入=日销售利润﹣每天固定支出的费用).
(1)求y与x之间的函数关系式;
(2)此水果超市销售该种水果的日净收入能否达到1560元?否能,请求出此时的销售单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个转盘中指针落在每个数字上的机会相等,现同时转动![]() 、
、![]() 两个转盘,停止后,指针各指向一个数字.小力和小明利用这两个转盘做游戏,若两数之积为非负数则小力胜;否则,小明胜.
两个转盘,停止后,指针各指向一个数字.小力和小明利用这两个转盘做游戏,若两数之积为非负数则小力胜;否则,小明胜.
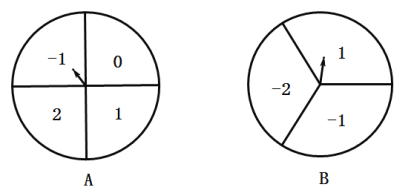
(1)画树状图或列表求出各人获胜的概率。
(2)这个游戏公平吗?说说你的理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD、AE,则∠EAD的度数为( )
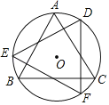
A.150°B.135°C.120°D.105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天早上,王霞从家出发步行上学,出发6分钟后王霞想起数学作业没有带,王霞立即打电话叫爸爸骑自行车把作业送来(接打电话和爸爸出门的时间忽略不计),同时王霞把速度降低到前面的一半.爸爸骑自行车追上王霞后立即掉头以原速赶往位于家的另一边的单位上班,王霞拿到作业后立即改为慢跑上学,慢跑的速度是最开始步行速度的2倍,最后王霞比爸爸早10分钟到达目的地.如图反映了王霞与爸爸之间的距离![]() (米)与王霞出发后时间
(米)与王霞出发后时间![]() (分钟)之间的关系,则王霞的家距离学校有__________米.
(分钟)之间的关系,则王霞的家距离学校有__________米.
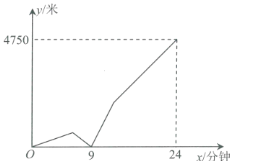
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作圆的一个内接矩形,并使其对角线的夹角为60°”的尺规作图过程
已知:⊙O
求作:矩形ABCD,使得矩形ABCD内接于⊙O,且其对角线AC,BD的夹角为60°.
作法:如图
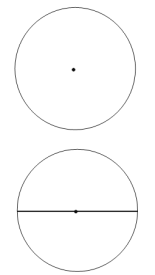
①作⊙O的直径AC;
②以点A为圆心,AO长为半径画弧,交直线AC上方的圆弧于点B;
③连接BO并延长交⊙O于点D;
所以四边形ABCD就是所求作的矩形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵点A,C都在⊙O上,
∴OA=OC
同理OB=OD
∴四边形ABCD是平行四边形
∵AC是⊙O的直径,
∴∠ABC=90° ( )(填推理的依据)
∴四边形ABCD是矩形
∵AB= =BO,
∴四边形ABCD四所求作的矩形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com