
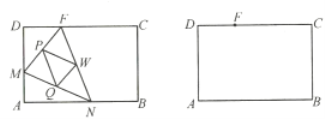
【题目】如图所示,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,沿射线
同时出发,沿射线![]() 、线段
、线段![]() 向点
向点![]() 的方向运动(点
的方向运动(点![]() 可运动到
可运动到![]() 的延长线上),当动点
的延长线上),当动点![]() 运动到点
运动到点![]() 时,
时,![]() 、
、![]() 两点同时停止运动.联结
两点同时停止运动.联结![]() 、
、![]() 、
、![]() ,过
,过![]() 三边的中点作
三边的中点作![]() .设动点
.设动点![]() 、
、![]() 的速度都是1个单位/秒,
的速度都是1个单位/秒,![]() 、
、![]() 运动的时间为
运动的时间为![]() 秒.试解答下列问题:
秒.试解答下列问题:
(1)说明![]() ;
;
(2)设![]() ,试问
,试问![]() 为何值时,
为何值时,![]() 为直角三角形?
为直角三角形?
(3)试用含![]() 的代数式表示
的代数式表示![]() ,并求当
,并求当![]() 为何值时,
为何值时,![]() 最小?求此时
最小?求此时![]() 的值.
的值.
【答案】(1)见解析;(2)当![]() 或
或![]() 时,
时,![]() 为直角三角形;(3)当
为直角三角形;(3)当![]() 时,
时, ![]() 的值最小,
的值最小,![]()
![]() ;当
;当![]() 时,
时,![]() 的值也最小,
的值也最小,![]() .
.
【解析】
(1)由根据题意可知P、W、Q分别是△FMN三边的中点,可得PW是△FMN的中位线,然后即可证明△FMN∽△QWP;
(2)由(1)得,△FMN∽△QWP,当△QWP为直角三角形时,△FMN为直角三角形,根据DM=BN=x,AN=6x,AM=4x,利用勾股定理求得FM2=4+x2,MN2=(4x)2+(6x)2,FN2=(4x)2+16,然后分①当MN2=FM2+FN2时,②当FN2=FM2+MN2时,③FM2=MN2+FN2时三种情况讨论即可.
(3)根据①当0≤x≤4,即M从D到A运动时,MN≥AN,AN=6x,故只有当x=4时,MN的值最小即可求得答案,②当4<x≤6时,MN2=AM2+AN2=(x4)2+(6x)2,解得x即可.
(1)由题意可知![]() 、
、![]() 、
、![]() 分别是
分别是![]() 三边的中点,
三边的中点,
![]() 是
是![]() 的中位线,即
的中位线,即![]() ,
,
同理![]() ,
,![]() .
.
![]() ,
,
同理![]() ,
,![]() .
.
![]()
(2)由(1)得,![]() ,
,
故当![]() 为直角三角形时,
为直角三角形时,![]() 为直角三角形,
为直角三角形,
反之亦然.

由题意可得![]() ,
,![]() ,
,![]() ,
,
由勾股定理分别得![]() ,
,![]() ,
,![]() .
.
过点N作NK⊥CD于K,
∴CK=BN=x,
∵CF=CDDF=62=4,
∴FK=4x,
∴FN2=NK2+FK2=(4x)2+16,
①当MN2=FM2+FN2时,(4x)2+(6x)2=4+x2+(4x)2+16,
解得x=![]() ,
,
②当![]()
![]() 时,
时,![]() ,
,
此方程无实数根.
③![]()
![]() 时,
时,![]() ,
,
解得![]() (不合题意,舍去),
(不合题意,舍去),
综上,当![]() 或
或![]() 时,
时,![]() 为直角三角形
为直角三角形
(3)①当![]() ,即
,即![]() 从
从![]() 到
到![]() 运动时,
运动时,![]() ,
,![]() ,
,
故只有当![]() 时,
时,![]() 的最小值,
的最小值,![]() 的值也最小,
的值也最小,
此时![]() ,
,![]() ;
;
②当![]() 时,
时,![]() ,
,
当![]() ,
,![]() 取得最小值2,
取得最小值2,
![]() 当
当![]() 时,
时,![]() 的值最小,此时
的值最小,此时![]() .
.
综上:当![]() 时,
时, ![]() 的值最小,
的值最小,![]()
![]() ;当
;当![]() 时,
时,![]() 的值也最小,
的值也最小,![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 中
中![]() 边的中点,
边的中点,![]() 于
于![]() ,以
,以![]() 为直径的
为直径的![]() 经过
经过![]() ,连接
,连接![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是
是![]() 的切线.其中正确的结论是( )
的切线.其中正确的结论是( )
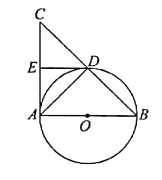
A.①②B.①②③C.②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为吸引市民组团去风景区旅游,观光旅行社推出了如下收费标准:

某单位员工去风景区旅游,共支付给旅行社旅游费用10500元,请问该单位这次共有多少员工去风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
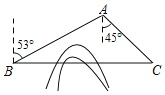
【题目】如图,C地在B地的正东方向,因有大山阻隔,由B地到C地需绕行A地,已知A地位于B地北偏东53°方向,距离B地516千米,C地位于A地南偏东45°方向.现打算打通穿山隧道,建成两地直达高铁,求建成高铁后从B地前往C地的路程.(结果精确到1千米)(参考数据:sin53°=![]() ,cos53°=
,cos53°=![]() ,tan53°=
,tan53°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
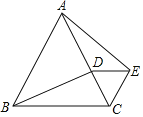
【题目】如图,△ABC是等边三角形,点D在AC边上,将△BCD绕点C旋转得到△ACE.
(1)求证:DE∥BC.
(2)若AB=8,BD=7,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
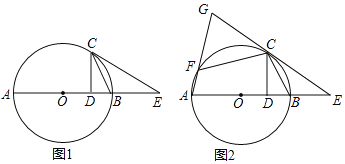
【题目】如图1,AB为⊙O的直径,C为⊙O上一点,连接CB,过C作CD⊥AB于点D,过点C作∠BCE,使∠BCE=∠BCD,其中CE交AB的延长线于点E.
(1)求证:CE是⊙O的切线.
(2)如图2,点F在⊙O上,且满足∠FCE=2∠ABC,连接AF井延长交EC的延长线于点G.
①试探究线段CF与CD之间满足的数量关系;
②若CD=4,BD=2,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙0上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC
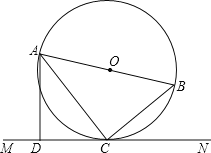
(1)猜想直线MN与⊙O的位置关系,并说明理由;
(2)若CD=6,cos∠ACD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与x轴、y轴分别交于点A、B,抛物线
与x轴、y轴分别交于点A、B,抛物线![]() 经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则
经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则![]() 的取值范围是____.
的取值范围是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com