
 如图,△ABC和△DCE都是等腰三角形,∠ACB=∠DCE=90°,点P、M、N分别为DE、BE、AD的中点.求证:MN=
如图,△ABC和△DCE都是等腰三角形,∠ACB=∠DCE=90°,点P、M、N分别为DE、BE、AD的中点.求证:MN=| 2 |
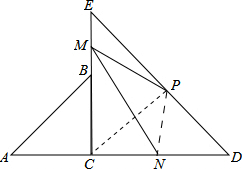
|
| 2 |


科目:初中数学 来源: 题型:
| A、5.71×108 |
| B、5.71×1010 |
| C、5.71×109 |
| D、5.71×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
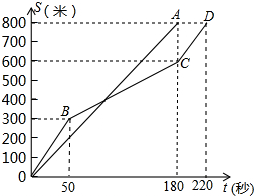 在某市初中学业水平考试体育学科800米能力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.下列说法错误的是( )
在某市初中学业水平考试体育学科800米能力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.下列说法错误的是( )| A、甲比乙先到达终点 |
| B、跑步过程中甲的速度不变 |
| C、起跑后400米内,乙始终在甲的前面 |
| D、在起跑后180米时,甲乙两人相遇 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com