
【题目】仔细阅读下面解方程组的方法,然后解决有关问题:解方程组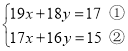 时,如果直接消元,那将会很繁琐,若采用下面的解法,则会简单很多.
时,如果直接消元,那将会很繁琐,若采用下面的解法,则会简单很多.
解:①-②,得:2x+2y=2,即x+y=1③
③×16,得:16x+16y=16④
②-④,得:x=-1
将x=-1
代入③得:y=2
∴原方程组的解为:![]()
(1)请你采用上述方法解方程组:![]()
(2)请你采用上述方法解关于x,y的方程组 ,其中
,其中![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)先把两式相减得出x+y的值,再把x+y的值与2010相乘,再用加减消元法求出x的值,用代入消元法求出y的值即可;
(2)先把两式相减得出(m-n)x+(m-n)y=m-n,的值,再用加减消元法求出x的值,用代入消元法求出y的值即可.
(1)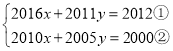
①-②,得:6x+6y=12,即x+y=2③,
③×2010,得:2010x+2010y=4020④,
④-②,得:y=404,
将y=404代入③得:x=-402,
∴方程组的解为:![]()
(2) 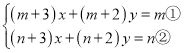
①-②,得:(m-n)x+(m-n)y=m-n,
∵m≠n,
∴x+y=1③,
③×(n+3),得:(n+3)x+(n+3)y=n+3④,
④-②,得:y=3,
将y=3代入③得:x=-2,
∴方程组的解为![]()


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,BC=2CD=2a,点E在边CD上,在矩形ABCD的左侧作矩形ECGF,使CG=2GF=2b,连接BD,CF,连结AF交BD于点H.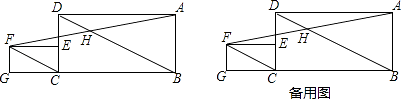
(1)求证:BD∥CF;
(2)求证:H是AF的中点;
(3)连结CH,若HC⊥BD,求a:b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]() ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于 ![]() 的一元二次方程
的一元二次方程 ![]() 的两个根,且OA>OB
的两个根,且OA>OB
(1)求cos∠ABC的值。
(2)若E为x轴上的点,且 ![]() ,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由
,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三个项点的坐标分别为A (3. 3),B (-3, 0), C (0. -2).
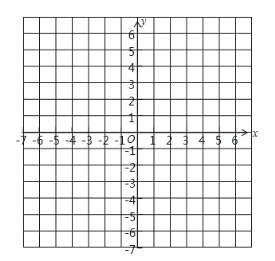
(1)在下面的平面直角坐标系中分别描出A,B, C三点,并画出△ABC;
(2)将(1)中的△ABC向上平移3个单位长度,向左中移2个单位长度,得到△![]() 在图中画出△
在图中画出△![]() ,请分别写出A1、B1、C1三点的坐标.
,请分别写出A1、B1、C1三点的坐标.
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图①、图②、图③均为顶点都在格点上的三角形(每个小方格的顶点叫格点),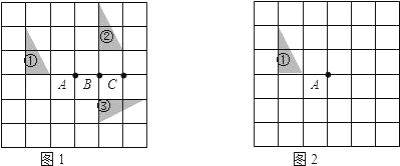
(1)在图1中,图①经过一次变换(填“平移”或“旋转”或“轴对称”)可以得到图②;
(2)在图1中,图③是可以由图②经过一次旋转变换得到的,其旋转中心是点(填“A”或 “B”或“C”);
(3)在图2中画出图①绕点A顺时针旋转90°后的图④.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元;购买
元;购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元.
元.
(1)求购买一个甲种文具、一个乙种文具各需多少元?
(2)若学校计划购买这两种文具共![]() 个,投入资金不少于
个,投入资金不少于![]() 元又不多于
元又不多于![]() 元,设购买甲种文具
元,设购买甲种文具![]() 个,求有多少种购买方案?
个,求有多少种购买方案?
(3)设学校投入资金![]() 元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com