
分析 (1)令y=$\frac{1}{2}$x2+x+c=0,根据抛物线y=$\frac{1}{2}$x2+x+c与x轴没有交点,则△<0,求出c的取值范围即可;
(2)根据反比例函数的性质直接得到双曲线y=$\frac{c}{x}$经过的象限.
解答 解:(1)令y=$\frac{1}{2}$x2+x+c=0,
∵抛物线y=$\frac{1}{2}$x2+x+c与x轴没有交点,
∴△=1-2c<0,
∴c>$\frac{1}{2}$;
(2)∵c>$\frac{1}{2}$,
∴双曲线y=$\frac{c}{x}$经过第一、三象限.
点评 本题主要考查了抛物线与x轴交点和反比例函数的性质的知识,解答本题要掌握抛物线与x轴没有交点,则△=b2-4ac<0,此题难度不大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 10m | B. | 12m | C. | 13m | D. | 15m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
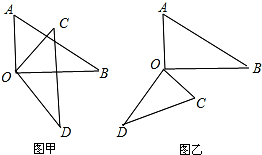 【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图甲所示的位置,请回答下面的问题.
【探究】将两个三角板的两个直角顶点O重合在一起,放置成如图甲所示的位置,请回答下面的问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com