
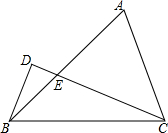
 如图,在△ABC中,BC=2$\sqrt{2}$,∠ABC=45°=2∠ECB,BD⊥CD,则(2BD)2=16-8$\sqrt{2}$.
如图,在△ABC中,BC=2$\sqrt{2}$,∠ABC=45°=2∠ECB,BD⊥CD,则(2BD)2=16-8$\sqrt{2}$. 分析 延长BD至F,使得DF=BD,连结CF交AB于G.根据中垂线的性质和等腰直角三角形的判定和性质得到CF=2$\sqrt{2}$,BG=CG=2,根据线段的和差求得FG=2$\sqrt{2}$-2,
在Rt△BGF中,根据勾股定理即可求解.
解答 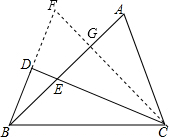 解:延长BD至F,使得DF=BD,连结CF交AB于G.
解:延长BD至F,使得DF=BD,连结CF交AB于G.
∵BD⊥CD,DF=BD,
∴CF=CB=2$\sqrt{2}$,∠DCF=∠ECB,
∵∠ABC=45°=2∠ECB,
∴∠BCG=45°,
∴△BCG是等腰直角三角形,
∵BC=2$\sqrt{2}$,
∴BG=CG=$\frac{\sqrt{2}}{2}$BC=2,
∴FG=2$\sqrt{2}$-2,
在Rt△BGF中,(2BD)2=BF2=BG2+FG2=22+(2$\sqrt{2}$-2)2=16-8$\sqrt{2}$.
故答案为:16-8$\sqrt{2}$.
点评 考查了勾股定理,中垂线的性质,等腰直角三角形的判定和性质,本题关键是作出辅助线构造直角三角形,难度较大.


科目:初中数学 来源: 题型:解答题
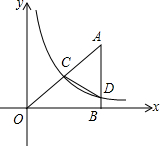 如图,在平面直角坐标系中,点A的横坐标为8,AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,交AB于点D.
如图,在平面直角坐标系中,点A的横坐标为8,AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
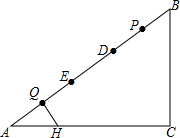 如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点E,D分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB,垂足为点Q,交AC于点H.当点E到达顶点B时,Q,P同时停止运动,则当△HDE为等腰三角形时,BP的值为$\frac{40}{21}$或$\frac{40}{11}$或5或$\frac{320}{103}$.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点E,D分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB,垂足为点Q,交AC于点H.当点E到达顶点B时,Q,P同时停止运动,则当△HDE为等腰三角形时,BP的值为$\frac{40}{21}$或$\frac{40}{11}$或5或$\frac{320}{103}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com