
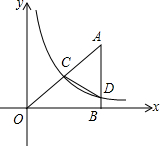
 如图,在平面直角坐标系中,点A的横坐标为8,AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,交AB于点D.
如图,在平面直角坐标系中,点A的横坐标为8,AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,交AB于点D.分析 (1)先根据锐角三角函数的定义,求出OA的值,然后根据勾股定理求出AB的值,然后由C点是OA的中点,求出C点的坐标,然后将C的坐标代入反比例函数y=$\frac{k}{x}$中,即可确定反比例函数解析式;
(2)作CE⊥x轴于点E,然后根据S四边形OCDB=S△OCE+S梯形CEBD即可求解.
解答 解:(1)∵A点的坐标为(8,y),
∴OB=8,
∵AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,
∴$\frac{OB}{OA}$=$\frac{4}{5}$,
∴OA=10,
由勾股定理得:AB=$\sqrt{O{A}^{2}-O{B}^{2}}$=6,
∵点C是OA的中点,且在第一象限内,
∴C(4,3),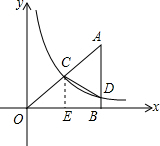
∵点C在反比例函数y=$\frac{k}{x}$的图象上,
∴k=12,
∴反比例函数解析式为:y=$\frac{12}{x}$;
(2)作CE⊥x轴于点E.则E的坐标是(4,0).
OE=BE=4,CE=3.
在y=$\frac{12}{x}$中,令x=8,解得y=$\frac{3}{2}$,则BD=$\frac{3}{2}$.
则S四边形OCDB=S△OCE+S梯形CEBD=$\frac{1}{2}$OE•CE+$\frac{1}{2}$(CE+BD)•BE=$\frac{1}{2}$×3×4+$\frac{1}{2}$(3+$\frac{3}{2}$)×4=6+9=15.
点评 本题考查了待定系数法求函数的解析式以及图形的面积的计算,在计算不规则的图形的面积时常用的方法是转化成规则图形的面积的和或差计算.


科目:初中数学 来源: 题型:解答题
| 捐款金额 | 5元 | 10元 | 15元 | 20元 |
| 捐款人数 | 10人 | 15人 |  | 5人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 得分 | 80 | 85 | 87 | 90 |
| 人数 | 1 | 3 | 2 | 2 |
| A. | 85,85 | B. | 87,85 | C. | 85,86 | D. | 85,87 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
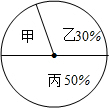 某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )
某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )| A. | 甲对应扇形的圆心角为72° | B. | 学生的总人数是900人 | ||
| C. | 甲比丙地区人数少180人 | D. | 丙比乙地区人数多180人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
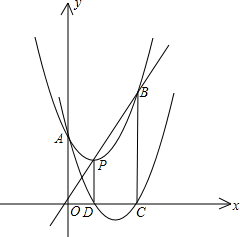 若将抛物线F:抛物线y=x2+bx$\frac{9}{2}$改成y=ax2+bx+c,抛物线的顶点为P,与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C.且a、b、c满足了b2=2ac
若将抛物线F:抛物线y=x2+bx$\frac{9}{2}$改成y=ax2+bx+c,抛物线的顶点为P,与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C.且a、b、c满足了b2=2ac查看答案和解析>>
科目:初中数学 来源: 题型:填空题
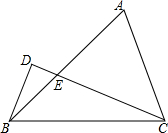 如图,在△ABC中,BC=2$\sqrt{2}$,∠ABC=45°=2∠ECB,BD⊥CD,则(2BD)2=16-8$\sqrt{2}$.
如图,在△ABC中,BC=2$\sqrt{2}$,∠ABC=45°=2∠ECB,BD⊥CD,则(2BD)2=16-8$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com