
【题目】一二六中学计划举行“最爱辽宁红色景点”调查活动,现随机抽取了部分学生进行主题为“你去过的景点是?”的问卷调查,要求学生必须从“![]() (辽沈战役纪念馆),
(辽沈战役纪念馆),![]() (鸭绿江断桥景区),
(鸭绿江断桥景区),![]() (战犯管理所旧址),
(战犯管理所旧址),![]() (大连市关向应故居纪念馆)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
(大连市关向应故居纪念馆)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
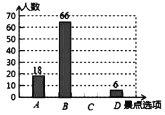
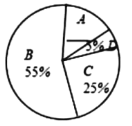
请你根据图中所提供的信息,完成下列问题:
(1)本次调查的学生人数为______人;
(2)在扇形统计图中,![]() 部分所占圆心角的度数为_____
部分所占圆心角的度数为_____![]() ;
;
(3)请直接将两个统计图补充完整;
(4)若该校共有2400名学生,估计该校最想去![]() 和
和![]() 的学生共有多少人?
的学生共有多少人?
【答案】(1)120;(2)18;(3)见解析;(4)1680
【解析】
(1)由B的人数除以其人数占被调查人数的百分比即可求解;
(2)用360°×D部分所占的百分比即可求解;
(3)用调查的学生总人数乘以C所占百分比得出C的人数,补全条形图;用1减去B、C、D所占的百分比得出A所占的百分比,补全扇形图;
(4)用样本中最想去![]() 和
和![]() 的学生所占的百分比之和乘总人数即可.
的学生所占的百分比之和乘总人数即可.
解:(1)本次调查的学生人数为66÷55%=120.
故答案为:120;
(2)在扇形统计图中,D部分所占圆心角的度数为360°×5%=18°.
故答案为:18;
(3)选择C的人数为:120×25%=30(人),
A所占的百分比为:155%25%5%=15%.
补全统计图如图: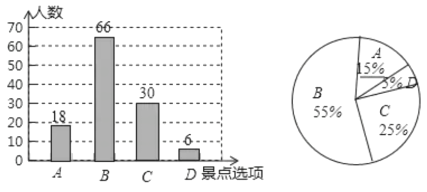
(4)(15%+55%)×2400=1680(人).
答:若该校共有2400名学生,估计该校最想去![]() 和
和![]() 的学生共有1680人.
的学生共有1680人.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同开凿一条隧道,甲队按一定的工作效率先施工,一段时间后,乙队从隧道的另一端按一定的工作效率加入施工,中途乙队遇到碎石层,工作效率降低,当乙队完成碎石层时恰好隧道被打通,此时甲队工作了45天.设甲、乙两队各自开凿隧道的长度为y(米),甲队的工作时间为x(天),y与x之间的函数图象如图所示.
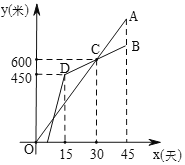
(1)求甲队的工作效率.
(2)求乙队在碎石层施工时y与x之间的函数关系式.
(3)求这条隧道的总长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生素养的重要途径.某中学为了了解全校学生课外阅读情况,随机抽查了200名学生,统计他们平均每天课外阅读时间(小时).根据每天课外阅读时间的长短分为A,B,C.D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
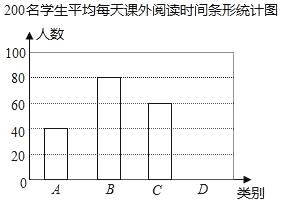
200名学生平均每天课外阅读时间统计表
类别 | 时间t(小时) | 人数 |
A | t<0.5 | 40 |
B | 0.5≤t<1 | 80 |
C | 1≤t<1.5 | 60 |
D | t≥1.5 | a |
(1)求表格中a的值,并在图中补全条形统计图:
(2)该校现有1800名学生,请你估计该校共有多少名学生课外阅读时间不少于1小时?
(3)请你根据上述信息对该校提出相应的建议
查看答案和解析>>
科目:初中数学 来源: 题型:
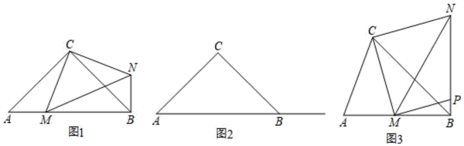
【题目】在△ABC中,∠ABC为锐角,点M为射线AB上一动点,连接CM,以点C为直角顶点,以CM为直角边在CM右侧作等腰直角三角形CMN,连接NB.
(1)如图1,图2,若△ABC为等腰直角三角形,
问题初现:①当点M为线段AB上不与点A重合的一个动点,则线段BN,AM之间的位置关系是 ,数量关系是 ;
深入探究:②当点M在线段AB的延长线上时,判断线段BN,AM之间的位置关系和数量关系,并说明理由;
(2)如图3,∠ACB≠90°,若当点M为线段AB上不与点A重合的一个动点,MP⊥CM交线段BN于点P,且∠CBA=45°,BC=![]() ,当BM= 时,BP的最大值为 .
,当BM= 时,BP的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
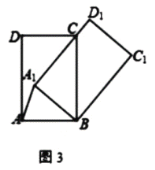
【题目】将矩形![]() 绕点
绕点![]() 顺时针旋转得到矩形
顺时针旋转得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]()
(1)当点![]() 落在
落在![]() 上时
上时
①如图1,若![]() ,求证:
,求证:![]()
②如图2,![]() 交
交![]() 于点
于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,
,
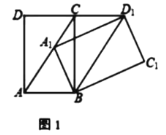
①如图3,当![]() 过点C时,则
过点C时,则![]() 的长=_____.
的长=_____.
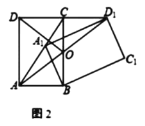
②当![]() 时,作
时,作![]() ,
,![]() 绕点
绕点![]() 转动,当直线
转动,当直线![]() 经过
经过![]() 时,直线
时,直线![]() 交边
交边![]() 于
于![]() ,
,![]() 的值=______.
的值=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 内接于
内接于![]() 为
为![]() 的直径,
的直径,![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() 作等边三角形
作等边三角形![]() 连接
连接![]() 为
为![]() 延长线上一点,满足
延长线上一点,满足![]() 延长
延长![]() 交
交![]() 于点
于点![]() ,在
,在![]() 存在一点
存在一点![]() ,使
,使![]() ,延长
,延长![]() 到点
到点![]() 使
使![]() 连接
连接![]() .
.
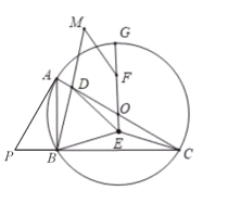
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:①![]() ;
;
②![]() ;
;
(3)若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
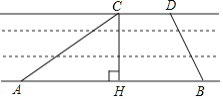
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
查看答案和解析>>
科目:初中数学 来源: 题型:
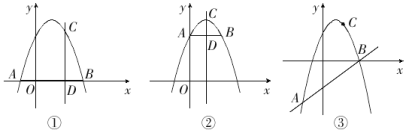
【题目】在平面直角坐标系中,直线AB与抛物线y=ax2+bx+c交于A,B(点A在点B的左侧)两点,点C是该抛物线上任意一点,过C点作平行于y轴的直线交AB于D,分别过点A,B作直线CD的垂线,垂足分别为点E,F.
特例感悟:
(1)已知:a=-2,b=4,c=6.
①如图①,当点C的横坐标为2,直线AB与x轴重合时,CD=____,|a|·AE·BF=___.
②如图②,当点C的横坐标为1,直线AB//x轴且过抛物线与y轴的交点时,CD=_____,|a|·AE·BF=_______.
③如图③,当点C的横坐标为2,直线AB的解析式为y=x-3时,CD=___,|a|·AE·BF=___.
猜想论证:
(2)由(1)中三种情况的结果,请你猜想在一般情况下CD与|a|·AE·BF之间的数量关系,并证明你的猜想.拓展应用.
(3)若a=-1,点A,B的横坐标分别为-4,2,点C在直线AB的上方的抛物线上运动(点C不与点A,B重合),在点C的运动过程中,利用(2)中的结论求出△ACB的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com