
【题目】在平面直角坐标系中,直线AB与抛物线y=ax2+bx+c交于A,B(点A在点B的左侧)两点,点C是该抛物线上任意一点,过C点作平行于y轴的直线交AB于D,分别过点A,B作直线CD的垂线,垂足分别为点E,F.
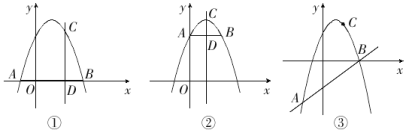
特例感悟:
(1)已知:a=-2,b=4,c=6.
①如图①,当点C的横坐标为2,直线AB与x轴重合时,CD=____,|a|·AE·BF=___.
②如图②,当点C的横坐标为1,直线AB//x轴且过抛物线与y轴的交点时,CD=_____,|a|·AE·BF=_______.
③如图③,当点C的横坐标为2,直线AB的解析式为y=x-3时,CD=___,|a|·AE·BF=___.
猜想论证:
(2)由(1)中三种情况的结果,请你猜想在一般情况下CD与|a|·AE·BF之间的数量关系,并证明你的猜想.拓展应用.
(3)若a=-1,点A,B的横坐标分别为-4,2,点C在直线AB的上方的抛物线上运动(点C不与点A,B重合),在点C的运动过程中,利用(2)中的结论求出△ACB的最大面积.
【答案】(1)①6,6;②2,2;③7,7;(2)![]() ,见解析;(3)27
,见解析;(3)27
【解析】
(1)①求得点A、B、C的坐标,得到点E、D、F三点重合,即可求得CD的长以及|a|·AE·BF的值;
②求得点A、B、C的坐标,得到点E、D、F三点重合,即可求得CD的长以及|a|·AE·BF的值;
③解方程组求得点A、B的坐标,再求得点C、D的坐标,即可求得CD的长以及|a|·AE·BF的值;
(2)利用参数法,设A、B、C三横坐标分别为:![]() ,直线AB的解析式为
,直线AB的解析式为![]() ,根据一元二次方程根与的关系,求得|a|·AE·BF
,根据一元二次方程根与的关系,求得|a|·AE·BF![]() ,再利用两点之间距离公式求得CD
,再利用两点之间距离公式求得CD![]() ,即可证明;
,即可证明;
(3)设点C的横坐标为![]() ,△ACB的面积为S,根据
,△ACB的面积为S,根据![]() ,点A,B的横坐标分别为-4,2,得到
,点A,B的横坐标分别为-4,2,得到![]() ,
,![]() ,
,![]() ,利用三角形面积公式即可得到关于x的二次函数,利用二次函数的最值即可求解.
,利用三角形面积公式即可得到关于x的二次函数,利用二次函数的最值即可求解.
(1)已知:![]() ,则抛物线的解析式为
,则抛物线的解析式为![]() ,
,
①令![]() ,则
,则![]() 或
或![]() ,
,
∴点A、B的坐标分别为![]() ,
,
∵点C的横坐标为2,
∴点C的坐标为![]()
∵直线AB与x轴重合,
∴点E、D、F三点重合,
如图:
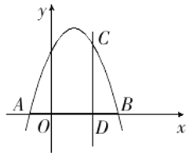
∴CD=6,
|a|·AE·BF=![]() ;
;
②令![]() ,则
,则![]() ,
,
∴点A的坐标为![]()
抛物线的对称轴为![]() ,
,
∵直线AB//x轴,
∴点B的坐标分别为![]()
∵点C的横坐标为1,
∴点C的坐标为![]()
∵直线AB//x轴,
∴点E、D、F三点重合,
如图:
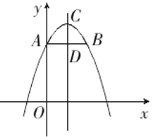
∴CD=8-6=2,
|a|·AE·BF=![]() ;
;
③解方程组 得:
得: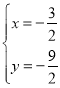 或
或![]() ,
,
∴点A、B的坐标分别为![]() ,
,
∵点C的横坐标为2,
∴点C的坐标为![]()
∵直线CD平行于y轴,
∴点D的横坐标为2,
把![]() 代入
代入![]() 得:
得:![]() ,
,
∴点D的坐标为![]()
如图:
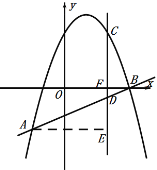
∴CD=CF-FD=6+1=7,
|a|·AE·BF=![]() ;
;
(2)数量关系为:![]() ,
,
理由如下:
设A、B、C三横坐标分别为:![]() ,直线AB的解析式为
,直线AB的解析式为![]() ,
,
联立方方程![]() 和
和![]() ,消去
,消去![]() 并整理得:
并整理得:
![]() ,
,
∵![]() 是方程的两根,
是方程的两根,
∴![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ·AE·BF=
·AE·BF=![]()
![]()
![]() ,
,
又∵点C的横坐标为t,
∴点C的坐标为![]()
∵直线CD平行于y轴,
∴点D的横坐标为t,
把![]() 代入
代入![]() 得:
得:![]() ,
,
∴点D的坐标为![]()
∴CD=![]()
=![]() ,
,
∴CD=![]() ·AE·BF;
·AE·BF;
(2)设点C的横坐标为![]() ,△ACB的面积为S,
,△ACB的面积为S,
过点C作CD平行于y轴交AB于D,
∵点A、B的横坐标分别为-4、2,
则![]() ,
,![]() ,
,
∵![]() ,点A,B的横坐标分别为-4,2,
,点A,B的横坐标分别为-4,2,
则抛物线的解析式为![]() ,
,
∴点A、B的坐标分别为![]() ,
,
设直线AB的解析式为![]() ,则
,则![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为![]() ,
,
∴点C的坐标为![]() 点D的坐标为
点D的坐标为![]()
∴![]() ,
,
∵![]() ,
,
由于![]() ,
,
∴当![]() 时,
时,![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一二六中学计划举行“最爱辽宁红色景点”调查活动,现随机抽取了部分学生进行主题为“你去过的景点是?”的问卷调查,要求学生必须从“![]() (辽沈战役纪念馆),
(辽沈战役纪念馆),![]() (鸭绿江断桥景区),
(鸭绿江断桥景区),![]() (战犯管理所旧址),
(战犯管理所旧址),![]() (大连市关向应故居纪念馆)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
(大连市关向应故居纪念馆)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
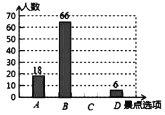
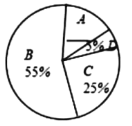
请你根据图中所提供的信息,完成下列问题:
(1)本次调查的学生人数为______人;
(2)在扇形统计图中,![]() 部分所占圆心角的度数为_____
部分所占圆心角的度数为_____![]() ;
;
(3)请直接将两个统计图补充完整;
(4)若该校共有2400名学生,估计该校最想去![]() 和
和![]() 的学生共有多少人?
的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图:
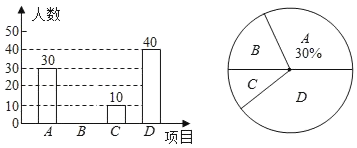
请结合图中所给信息,解答下列问题
(1)本次调查的学生共有 人;
(2)补全条形统计图;
(3)七年级一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农村初中2018年选拔了7名学生参加县级“综合体能”竞赛,该校2019年仍选了7名学生准备参赛,为了了解这7名学生的实力,在3月1日进行了一次与去年项目、评分方法完全一样的测试,两年成绩(单位:分)如下表:
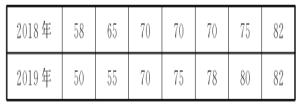
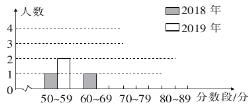
(1)请根据表中的数据补全条形统计图.
(2)分别求出两年7名学生成绩的中位数和平均数.
(3)经计算,2019年的7名学生成绩的方差s22019=136.86,那么哪年的7名学生的成绩较为整齐?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数![]() (a,b为常数,且
(a,b为常数,且![]() )与反比例函数
)与反比例函数![]() (m为常数,且
(m为常数,且![]() )的图象交于点A(﹣2,1)、B(1,n).
)的图象交于点A(﹣2,1)、B(1,n).

(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算2![]() ﹣3
﹣3![]() ﹣5
﹣5![]() +(﹣3
+(﹣3![]() )
)
(2)某同学做一道数学题:“两个多项式A、B,B=3x2﹣2x﹣6,试求A+B”,这位同学把“A+B”看成“A﹣B”,结果求出答案是﹣8x2+7x+10,那么A+B的正确答案是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各问题中,两个变量之间的关系不是反比例函数的是
A. 小明完成100m赛跑时,时间t(s)与跑步的平均速度v(m/s)之间的关系.
B. 菱形的面积为48cm2,它的两条对角线的长为y(cm)与x(cm)的关系.
C. 一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的体积V之间的关系.
D. 压力为600N时,压强p与受力面积S之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com