
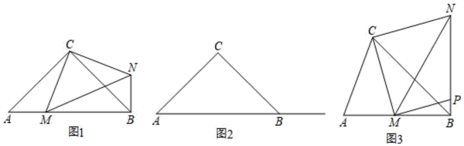
【题目】在△ABC中,∠ABC为锐角,点M为射线AB上一动点,连接CM,以点C为直角顶点,以CM为直角边在CM右侧作等腰直角三角形CMN,连接NB.
(1)如图1,图2,若△ABC为等腰直角三角形,
问题初现:①当点M为线段AB上不与点A重合的一个动点,则线段BN,AM之间的位置关系是 ,数量关系是 ;
深入探究:②当点M在线段AB的延长线上时,判断线段BN,AM之间的位置关系和数量关系,并说明理由;
(2)如图3,∠ACB≠90°,若当点M为线段AB上不与点A重合的一个动点,MP⊥CM交线段BN于点P,且∠CBA=45°,BC=![]() ,当BM= 时,BP的最大值为 .
,当BM= 时,BP的最大值为 .
【答案】(1)①AM⊥BN,AM=BN;②AM与BN位置关系是AM⊥BN,数量关系是AM=BN,见解析;(2)2,1.
【解析】
(1)问题初现:①由“SAS”证明△ACM≌△BCN,可得结论;
深入探究:②由“SAS”证明△ACM≌△BCN,可得结论;
(2)过点C作CE⊥AB于点E,过点N作NF⊥CE于点F,则FN∥AB,通过证明四边形FNBE是矩形,可得CE=BE=4,∠CEM=∠ABN=90°,通过证明△CEM∽△MBP,可得![]() ,即BP=
,即BP=![]() =﹣
=﹣![]() (BM﹣2)2+1,由二次函数的性质可求解.
(BM﹣2)2+1,由二次函数的性质可求解.
解:(1)问题初现:①AM与BN位置关系是AM⊥BN,数量关系是AM=BN.
理由:∵△ABC,△CMN为等腰直角三角形,
∴∠ACB=∠MCN=90°,AC=BC,CM=CN,∠CAB=∠CBA=45°
∴∠ACM=∠BCN,且 AC=BC,CM=CN,
∴△ACM≌△BCN (SAS)
∴∠CAM=∠CBN=45°,AM=BN.
∵∠CAB=∠CBA=45°,
∴∠ABN=45°+45°=90°,即 AM⊥BN
故答案为:AM⊥BN; AM=BN;
深入探究:②当点M在线段AB的延长线上时,AM与BN位置关系是AM⊥BN,数量关系是AM=BN.
理由如下:如图,

∵△ABC,△CMN为等腰直角三角形,
∴∠ACB=∠MCN=90°,AC=BC,CM=CN,∠CAB=∠CBA=45°
∴∠ACM=∠BCN,且 AC=BC,CM=CN,
∴△ACM≌△BCN (SAS)
∴∠CAM=∠CBN=45°,AM=BN.
∵∠CAB=∠CBA=45°,
∴∠ABN=45°+45°=90°,即 AM⊥BN;
(2)如图,过点C作CE⊥AB于点E,过点N作NF⊥CE于点F,则FN∥AB

∵△MCN是等腰直角三角形
∴CM=CN,∠MCN=90°
∴∠ECM+∠FCN=90°,且∠ECM+∠CME=90°
∴∠FCN=∠CME,且CM=CN,∠F=∠CEM=90°
∴△CNF≌△CME(AAS)
∴FN=EC,EM=CF
∵BC=![]() ,CE⊥AB,∠CBA=45°
,CE⊥AB,∠CBA=45°
∴CE=BE=4,
∴FN=BE=CE,且FN∥BA
∴四边形FNBE是平行四边形,且∠F=90°
∴四边形FNBE是矩形
∴∠CEM=∠ABN=90°
∴∠PMB+∠MPB=90°
∵CM⊥MP
∴∠CME+∠PMB=90°
∴∠CME=∠MPB,且∠CEM=∠ABN=90°
∴△CEM∽△MBP
∴![]()
∴BP=![]() =﹣
=﹣![]() (BM﹣2)2+1
(BM﹣2)2+1
∴当BM=2时,BP有最大值为1.
故答案为:2,1


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
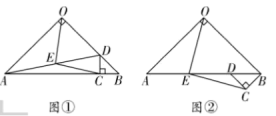
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
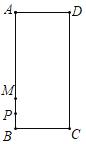
【题目】如图,矩形ABCD中,动点P沿B→A→D→C→B路线运动,点M是AB边上的一点,且MB=![]() AB,已知AB=4,BC=2,AP=2MP,则点P到边AD的距离为_______.
AB,已知AB=4,BC=2,AP=2MP,则点P到边AD的距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AE平分∠BAC交BC于E,CD⊥AE交AE延长线于D,连接BD,若BD=CD,⊙O是以AE为直径的△ABE的外接圆,与AC交于点H.

(1)求证:BD为⊙O的切线;
(2)设⊙O的半径为1,BF平分∠ABC交AE于G,交⊙O于F;
①求![]() 的值.
的值.
②求BE2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有150名女生,为了解该年级女生实心球成绩(单位:米)和一分钟仰卧起坐成绩(单位:个)的情况,从中随机抽取30名女生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a. 实心球成绩的频数分布表如下:
分组 |
|
|
|
|
|
|
频数 | 2 | m | 10 | 6 | 2 | 1 |
b. 实心球成绩在![]() 这一组的是:
这一组的是:
a7.0 7.0 7.0 7.1 7.1 7.1 7.2 7.2 7.3 7.3
c. 一分钟仰卧起坐成绩如下图所示:
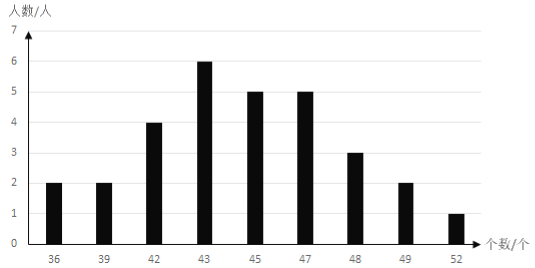
根据以上信息,回答下列问题:
(1) ①表中m的值为__________;
②一分钟仰卧起坐成绩的中位数为__________;
(2)若实心球成绩达到7.2米及以上时,成绩记为优秀.
①请估计全年级女生实心球成绩达到优秀的人数;
②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有3名女生的一分钟仰卧起坐成绩未抄录完整,但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一二六中学计划举行“最爱辽宁红色景点”调查活动,现随机抽取了部分学生进行主题为“你去过的景点是?”的问卷调查,要求学生必须从“![]() (辽沈战役纪念馆),
(辽沈战役纪念馆),![]() (鸭绿江断桥景区),
(鸭绿江断桥景区),![]() (战犯管理所旧址),
(战犯管理所旧址),![]() (大连市关向应故居纪念馆)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
(大连市关向应故居纪念馆)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
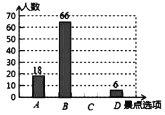
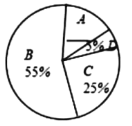
请你根据图中所提供的信息,完成下列问题:
(1)本次调查的学生人数为______人;
(2)在扇形统计图中,![]() 部分所占圆心角的度数为_____
部分所占圆心角的度数为_____![]() ;
;
(3)请直接将两个统计图补充完整;
(4)若该校共有2400名学生,估计该校最想去![]() 和
和![]() 的学生共有多少人?
的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由几个相同的小正方形搭成的几何体,搭成这个几何体需要( )个小正方体,在保持主视图和左视图不变的情况下,最多可以拿掉( )个小正方体

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农村初中2018年选拔了7名学生参加县级“综合体能”竞赛,该校2019年仍选了7名学生准备参赛,为了了解这7名学生的实力,在3月1日进行了一次与去年项目、评分方法完全一样的测试,两年成绩(单位:分)如下表:
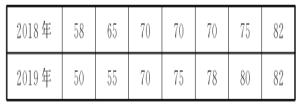
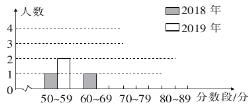
(1)请根据表中的数据补全条形统计图.
(2)分别求出两年7名学生成绩的中位数和平均数.
(3)经计算,2019年的7名学生成绩的方差s22019=136.86,那么哪年的7名学生的成绩较为整齐?请通过计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com