
【题目】某年级共有150名女生,为了解该年级女生实心球成绩(单位:米)和一分钟仰卧起坐成绩(单位:个)的情况,从中随机抽取30名女生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a. 实心球成绩的频数分布表如下:
分组 |
|
|
|
|
|
|
频数 | 2 | m | 10 | 6 | 2 | 1 |
b. 实心球成绩在![]() 这一组的是:
这一组的是:
a7.0 7.0 7.0 7.1 7.1 7.1 7.2 7.2 7.3 7.3
c. 一分钟仰卧起坐成绩如下图所示:
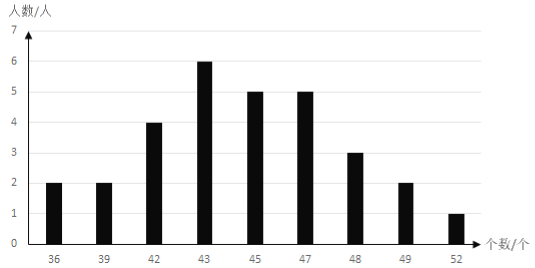
根据以上信息,回答下列问题:
(1) ①表中m的值为__________;
②一分钟仰卧起坐成绩的中位数为__________;
(2)若实心球成绩达到7.2米及以上时,成绩记为优秀.
①请估计全年级女生实心球成绩达到优秀的人数;
②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有3名女生的一分钟仰卧起坐成绩未抄录完整,但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.
【答案】(1)①![]() ;②
;②![]() ;(2)①估计全年级女生实心球成绩达到优秀的人数约为65人;②同意,理由详见解析.
;(2)①估计全年级女生实心球成绩达到优秀的人数约为65人;②同意,理由详见解析.
【解析】
(1)①因为已知检测总人数和其它组的频数,所以可以得到m;
②结合题意,根据中位数求法即可得到答案;
(2)①由题意得到参与测试女生实心球成绩达到优秀(人)的百分比,再乘以150,即可得出答案.
②结合题中数据,即可得出答案.
解:(1)①因为已知检测总人数为30人,所以m=30-(2+10+6+2+1)=9;
②根据中位数求法,由于数据为30个,所以去第15和16位的平均数,即45;
(2)①由题意得到参与测试女生实心球成绩达到优秀(人)的百分比为![]() ,所以可得
,所以可得![]() (人).
(人).
答:估计全年级女生实心球成绩达到优秀的人数约为65人.
②同意,理由答案不唯一,如:如果女生![]() 的仰卧起坐成绩未达到优秀,那么至少
的仰卧起坐成绩未达到优秀,那么至少![]() 有可能两项测试成绩都达到优秀,这与恰有4人两项测试成绩都达到优秀矛盾,因为女生
有可能两项测试成绩都达到优秀,这与恰有4人两项测试成绩都达到优秀矛盾,因为女生![]() 的一分钟仰卧起坐成绩达到了优秀.
的一分钟仰卧起坐成绩达到了优秀.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点C在
,点C在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点C作
,过点C作![]() 于点F,交
于点F,交![]() 于点G,过C作
于点G,过C作![]() 交
交![]() 的延长线于点E.
的延长线于点E.
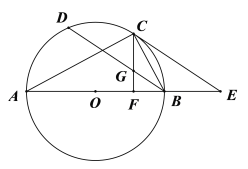
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会实践活动中,负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:x),并绘制了样本的频数分布表如下:
月均用水量 | 2≤x<3 | 3≤x<4 | 4≤x<5 | 5≤x<6 | 6≤x<7 | 7≤x<8 | 8≤x<9 |
频数 | 2 | 12 | ① | 10 | ② | 3 | 2 |
百分比 | 4% | 24% | 30% | 20% | ③ | 6% | 4% |
(1)请根据题中已有的信息补全频数分布表:① ;② ;③
(2)如果家庭月均用水量在5≤x<8范围内为中等用水量家庭,请你通过样本估计,总体中的中等用水量家庭大约有多少户?
(3)记月均用水量在2≤x<3范围内的两户为a1,a2,在8≤x<9范围内的2户为b1,b2,现从这4户家庭中任意抽取2户,请你通过列表或画树状图求出抽取的2户家庭来自不同范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
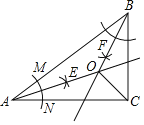
【题目】如图,在△ABC中,AB=10,AC=8,BC=6.按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB,AC于点M,N;
②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧交于点E;
MN的长为半径作弧,两弧交于点E;
③作射线AE;
④以同样的方法作射线BF,AE交BF于点O,连结OC,则OC为( )
A.2![]() B.2C.
B.2C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
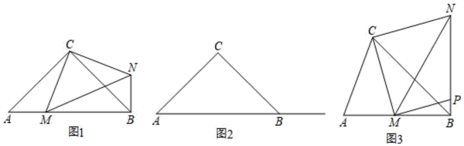
【题目】在△ABC中,∠ABC为锐角,点M为射线AB上一动点,连接CM,以点C为直角顶点,以CM为直角边在CM右侧作等腰直角三角形CMN,连接NB.
(1)如图1,图2,若△ABC为等腰直角三角形,
问题初现:①当点M为线段AB上不与点A重合的一个动点,则线段BN,AM之间的位置关系是 ,数量关系是 ;
深入探究:②当点M在线段AB的延长线上时,判断线段BN,AM之间的位置关系和数量关系,并说明理由;
(2)如图3,∠ACB≠90°,若当点M为线段AB上不与点A重合的一个动点,MP⊥CM交线段BN于点P,且∠CBA=45°,BC=![]() ,当BM= 时,BP的最大值为 .
,当BM= 时,BP的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面改善公园环境,现招标建设某全长960米绿化带,![]() 两个工程队的竞标,
两个工程队的竞标,![]() 队平均每天绿化长度是
队平均每天绿化长度是![]() 队的2倍,若由一个工程队单独完成绿化,
队的2倍,若由一个工程队单独完成绿化,![]() 队比
队比![]() 队要多用6天,
队要多用6天,
(1)分别求出![]() 两队平均每天绿化长度.
两队平均每天绿化长度.
(2)若决定由两个工程队共同合作绿化,要求至多5天完成绿化任务,两队都按(1)中的工作效率绿化完2天时,现又多出510米需要绿化,为了不超过5天时限,两队决定从第3天开始,各自都提高工作效率,且![]() 队平均每天绿化长度仍是
队平均每天绿化长度仍是![]() 队的2倍,则
队的2倍,则![]() 队提高工作效率后平均每天至少绿化多少米?
队提高工作效率后平均每天至少绿化多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
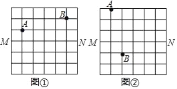
【题目】图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,点A、B、M、N均落在格点上,在图①、图②给定的网格中按要求作图.
(1)在图①中的格线MN上确定一点P,使PA与PB的长度之和最小
(2)在图②中的格线MN上确定一点Q,使∠AQM=∠BQM.
要求:只用无刻度的直尺,保留作图痕迹,不要求写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整).

(1)这次调查中,一共调查了________名学生;
(2)请补全两幅统计图;
(3)若有3名喜欢跳绳的学生,1名喜欢足球的学生组队外出参加一次联谊活动,欲从中选出2人担任组长(不分正副),求一人是喜欢跳绳、一人是喜欢足球的学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com