
【题目】为全面改善公园环境,现招标建设某全长960米绿化带,![]() 两个工程队的竞标,
两个工程队的竞标,![]() 队平均每天绿化长度是
队平均每天绿化长度是![]() 队的2倍,若由一个工程队单独完成绿化,
队的2倍,若由一个工程队单独完成绿化,![]() 队比
队比![]() 队要多用6天,
队要多用6天,
(1)分别求出![]() 两队平均每天绿化长度.
两队平均每天绿化长度.
(2)若决定由两个工程队共同合作绿化,要求至多5天完成绿化任务,两队都按(1)中的工作效率绿化完2天时,现又多出510米需要绿化,为了不超过5天时限,两队决定从第3天开始,各自都提高工作效率,且![]() 队平均每天绿化长度仍是
队平均每天绿化长度仍是![]() 队的2倍,则
队的2倍,则![]() 队提高工作效率后平均每天至少绿化多少米?
队提高工作效率后平均每天至少绿化多少米?
【答案】(1)160,80;(2)110
【解析】
(1)设B队平均每天绿化长度是x米,则A队平均每天绿化长度是2x米,依据由一个工程队单独完成绿化,B队比A队要多用6天,列分式方程求解即可;
(2)设B队提高工作效率后平均每天至少绿化a米,则A队平均每天绿化长度是2a米,依据后3天完成的绿化不少于990米,列不等式求解即可.
(1)设B队平均每天绿化长度是x米,则A队平均每天绿化长度是2x米,
依题意得:![]() ,
,
解得x=80,
经检验x=80是原方程的根,且符合题意,
∴2x=160,
答:A,B两队平均每天绿化长度分别为160米和80米.
(2)两队都按(1)中的工作效率绿化2天完成:2(160+80)=480(米),
2天后需要绿化:960480+510=990(米),
设B队提高工作效率后平均每天至少绿化a米,则A队平均每天绿化长度是2a米,
依题意得:3(a+2a)≥990,
解得:a≥110
∴B队提高工作效率后平均每天至少绿化110米.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 的速度向终点
的速度向终点![]() 运动.点
运动.点![]() 从
从![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 的速度向点
的速度向点![]() 运动、同时当点
运动、同时当点![]() 运动停止时,点
运动停止时,点![]() 随之停止运动.过点
随之停止运动.过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() ,将
,将![]() 绕
绕![]() 的中点旋转180°得到
的中点旋转180°得到![]() .过点
.过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,以
,以![]() 为边向右下方作正方形
为边向右下方作正方形![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
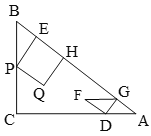
(1)直接写出![]() 的长度(用含
的长度(用含![]() 的代数式表示).
的代数式表示).
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值.
的值.
(3)当正方形![]() 与
与![]() 有重合部分时,求正方形
有重合部分时,求正方形![]() 与
与![]() 重合图形部分的周长
重合图形部分的周长![]() 与时间
与时间![]() 的函数解析式.
的函数解析式.
(4)当直线![]() 与
与![]() 的某一边垂直时,直接写出
的某一边垂直时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为△ABC外接圆的圆心,以AB为腰作等腰△ABD,使底边AD经过点O,并分别交BC于点E、交⊙O于点F,若∠BAD=30°.
(1)求证:BD是⊙O的切线;
(2)当CA2=CECB时,
①求∠ABC的度数;
②![]() 的值.
的值.
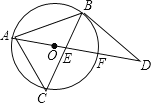
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有150名女生,为了解该年级女生实心球成绩(单位:米)和一分钟仰卧起坐成绩(单位:个)的情况,从中随机抽取30名女生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a. 实心球成绩的频数分布表如下:
分组 |
|
|
|
|
|
|
频数 | 2 | m | 10 | 6 | 2 | 1 |
b. 实心球成绩在![]() 这一组的是:
这一组的是:
a7.0 7.0 7.0 7.1 7.1 7.1 7.2 7.2 7.3 7.3
c. 一分钟仰卧起坐成绩如下图所示:
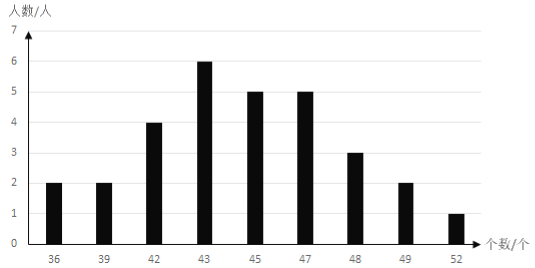
根据以上信息,回答下列问题:
(1) ①表中m的值为__________;
②一分钟仰卧起坐成绩的中位数为__________;
(2)若实心球成绩达到7.2米及以上时,成绩记为优秀.
①请估计全年级女生实心球成绩达到优秀的人数;
②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有3名女生的一分钟仰卧起坐成绩未抄录完整,但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为![]() 的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则
的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则![]() 长为______时,能围成的矩形区域
长为______时,能围成的矩形区域![]() 的面积最大.
的面积最大.
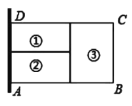
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由几个相同的小正方形搭成的几何体,搭成这个几何体需要( )个小正方体,在保持主视图和左视图不变的情况下,最多可以拿掉( )个小正方体

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
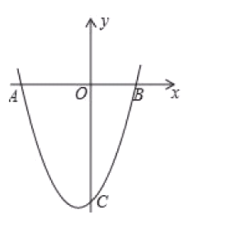
【题目】已知抛物线![]() 的对称轴与
的对称轴与![]() 轴的交点横坐标是分式方程
轴的交点横坐标是分式方程![]() 的解,若抛物线与
的解,若抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ,与
,与![]() 轴的交点
轴的交点![]()
(1)求抛物线![]() 的解析式;
的解析式;
(2)若点![]() 坐标为
坐标为![]() ,连结
,连结![]() ,若点
,若点![]() 是线段
是线段![]() 上的一个动点,求
上的一个动点,求![]() 的最小值.
的最小值.
(3)连结![]() 过点
过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 在第三象限中的抛物线上取点
在第三象限中的抛物线上取点![]() 过点
过点![]() 作直线
作直线![]() 的垂线交直线
的垂线交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,已知
,已知![]() .
.
①求点![]() 的坐标;
的坐标;
②在抛物线上是否存在一点![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地政府计划为农户购买农机设备提供补贴.其中购买Ⅰ型、Ⅱ型设备农民所投资的金额与政府补贴的额度存在下表所示的函数对应关系.
型号 金额 | Ⅰ型设备 | Ⅱ型设备 | |||
投资金额x(万元) | x | 5 | x | 2 | 4 |
补贴金额y(万元) | y1=kx(k≠0) | 2 | y2=ax2+bx(a≠0) | 2.8 | 4 |
(1)分别求y1和y2的函数解析式;
(2)有一农户共投资10万元购买Ⅰ型、Ⅱ型两种设备,两种设备的投资均为整数万元,要想获得最大补贴金额,应该如何购买?能获得的最大补贴金额为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( )
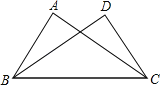
A.∠ABC=∠DCBB.∠ABD=∠DCA
C.AC=DBD.AB=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com