
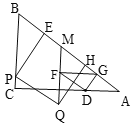
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 的速度向终点
的速度向终点![]() 运动.点
运动.点![]() 从
从![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 的速度向点
的速度向点![]() 运动、同时当点
运动、同时当点![]() 运动停止时,点
运动停止时,点![]() 随之停止运动.过点
随之停止运动.过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() ,将
,将![]() 绕
绕![]() 的中点旋转180°得到
的中点旋转180°得到![]() .过点
.过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,以
,以![]() 为边向右下方作正方形
为边向右下方作正方形![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
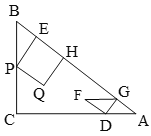
(1)直接写出![]() 的长度(用含
的长度(用含![]() 的代数式表示).
的代数式表示).
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值.
的值.
(3)当正方形![]() 与
与![]() 有重合部分时,求正方形
有重合部分时,求正方形![]() 与
与![]() 重合图形部分的周长
重合图形部分的周长![]() 与时间
与时间![]() 的函数解析式.
的函数解析式.
(4)当直线![]() 与
与![]() 的某一边垂直时,直接写出
的某一边垂直时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() =52t-30;当
=52t-30;当![]() 时,
时,![]() =12t;当
=12t;当![]() 时,
时,![]() =-6t+15;(4)
=-6t+15;(4)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)利用勾股定理可求出AB的长,可得cosA=![]() ,利用距离=速度×时间可求出AD=5t,利用∠A的余弦值即可得答案;
,利用距离=速度×时间可求出AD=5t,利用∠A的余弦值即可得答案;
(2)如图,由旋转的性质可得四边形AGFD是平行四边形,∠FDG=∠AGD=90°,可得∠HGF=∠A,根据三角函数的定义可得tan∠B=![]() ,根据距离=速度×时间可求出BE=4t,利用∠B的正切值可用t表示出PE的长,由正方形的性质可得EH=PE,当点F落在
,根据距离=速度×时间可求出BE=4t,利用∠B的正切值可用t表示出PE的长,由正方形的性质可得EH=PE,当点F落在![]() 上时可得四边形FDGH是矩形,可得FD=HG,即可证明HG=AG,根据BE+EH+HG+AG=AB=10列方程即可求出t值;
上时可得四边形FDGH是矩形,可得FD=HG,即可证明HG=AG,根据BE+EH+HG+AG=AB=10列方程即可求出t值;
(3)先分别求出DG与HQ重合、点F落在PE上、DG与PE重合时的t值,再根据各时间段中l与t当关系式即可;
(4)分QF⊥BC、QF⊥AB、QF⊥AC三种情况,利用∠A的三角函数及线段的和差关系分别求出t值即可.
(1)∵AC=8,BC=6,
∴AB=![]() =10,
=10,
∴cos∠A=![]() ,sin∠A=
,sin∠A=![]() ,tan∠A=
,tan∠A=![]() ,
,
∵点D的速度为每秒5cm,
∴AD=5t,
∴AG=AD·cosA=5t×![]() =4t.
=4t.
(2)∵将![]() 绕
绕![]() 的中点旋转180°得到
的中点旋转180°得到![]() ,
,
∴四边形AGFD是平行四边形,∠FDG=∠AGD=90°,AG=FD,
∵点![]() 落在
落在![]() 上,DG⊥AB,四边形EPQH是正方形,
上,DG⊥AB,四边形EPQH是正方形,
∴∠FHG=∠DGH=∠FDG=90°,
∴四边形FDGH是矩形,
∴FD=HG,
∴HG=AG=4t,
∵AC=8,BC=6,∠BCA=90°,
∴tan∠B=![]() =
=![]() ,
,
∵点E的速度为每秒4cm,
∴BE=4t,
∴PE=BE·tan∠B=![]() t,
t,
∵四边形EPQH是正方形,
∴EH=PE=![]() t,
t,
∵BE+EH+HG+AG=AB=10,
∴4t+![]() t+4t+4t=10,
t+4t+4t=10,
解得:![]() .
.
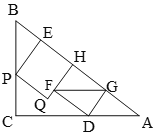
(3)∵AD=5t,AG=4t,
∴DG=3t,
如图,当DG与HQ重合时,
∵BE=4t,EH=PE=![]() t,AG=4t,
t,AG=4t,
∴4t+![]() t+4t=10,
t+4t=10,
解得:t=![]() ,
,
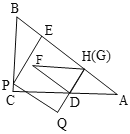
如图,当点F落在PE上时,
∵BE=4t,EG=DF=4t,AG=4t,
∴4t+4t+4t=10,
解得:t=![]() ,
,
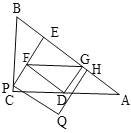
如图,当DG与PE重合时,
∵BE=4t,AG=4t,
∴4t+4t=10,
解得:t=![]() ,
,
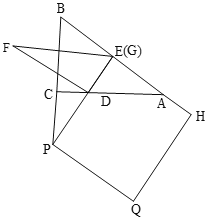
①如图,当![]() 时,FD、FG分别交QH于M、N,
时,FD、FG分别交QH于M、N,
∵BE=4t,EH=PE=![]() t,AG=4t,
t,AG=4t,
∴HG=10-4t-4t-![]() t=10-
t=10-![]() t,
t,
∵四边形MDGH是矩形,
∴MB=GH=10-![]() t,
t,
∴FM=FD-MD=4t-(10-![]() t)=
t)=![]() t-10,
t-10,
∵∠F=∠A,
∴MN=FM·tan∠A=![]() FM=13t-
FM=13t-![]() ,FN=
,FN=![]() =
=![]() FM=
FM=![]() ,
,
∴l=FM+MN+FN=52t-30.
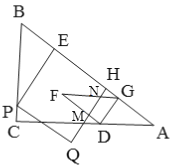
②当![]() 时,重合部分的周长即是△FDG当周长,
时,重合部分的周长即是△FDG当周长,
∴l=3t+4t+5t=12t.
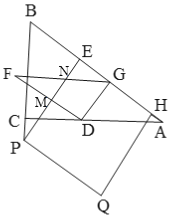
③如图,当![]() 时,FD、FG分别交PE于M、N,
时,FD、FG分别交PE于M、N,
∵BE=4t,AG=4t,
∴EG=MD=10-8t,
∵∠EGN=∠A,
∴NE=EG·tan∠A=![]() -6t,NG=
-6t,NG=![]() =
=![]() -10t,
-10t,
∴MN=MN-NE=DG-NE=3t-(![]() -6t)=9t-
-6t)=9t-![]() ,
,
∴l=MN+NG+DG+MD=9t-![]() +
+![]() -10t+3t+10-8t=-6t+15,
-10t+3t+10-8t=-6t+15,
综上所述:当![]() 时,l=52t-30;当
时,l=52t-30;当![]() 时,l=12t;当
时,l=12t;当![]() 时,l= -6t+15.
时,l= -6t+15.
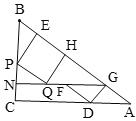
(4)①如图,当FQ⊥BC时,
∵四边形AGFD是平行四边形,
∴FG//AC,
∵∠BCA=90°,
∴GF⊥BC,
∴点Q在直线GF上,
∵AG=4t, QH=PE=EH=![]() t,
t,
∴HG=10-4t-4t-![]() t=10-
t=10-![]() t,
t,
∵∠FDN=∠A,
∴QH=HG·tan∠A,即![]() t=
t=![]() (10-
(10-![]() t),
t),
解得:![]() ,
,
②由(2)可知,当点F落在QH上时,DF⊥AB,此时![]() ,
,
③如图,当FQ⊥AC时,直线FQ交AB于M,
∵FQ⊥AC,FG//AC,
∴FQ⊥FG,
∵∠A+∠QMH=90°,∠MQH+∠QMH=90°,
∴∠MQH=∠A,
∵QH=PE=![]() t,FG=AD=5t,
t,FG=AD=5t,
∴MH=QH·tan∠A=4t,MG=![]() =
=![]() t,
t,
∵BE=4t,AG=4t,EH=![]() t,
t,
∴HG=10-![]() t,
t,
∵MG=MH+HG,即![]() t=4t+10-
t=4t+10-![]() t,
t,
解得:![]() ,
,
综上所述:直线![]() 与
与![]() 的某一边垂直时,
的某一边垂直时,![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6与反比例函数![]() 的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的表达式;
(2)观察图象,直接写出当x>0时,不等式2x+6-![]() <0的解集;
<0的解集;
(3)当n为何值时,△BMN的面积最大?最大值是多少?
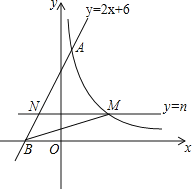
查看答案和解析>>
科目:初中数学 来源: 题型:
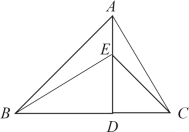
【题目】已知:如图,AD⊥BC,垂足为D,AD=BD,点E在AD上,∠CED=45°,
(1)请写出图中相等的线段: .(不包括已知条件中的相等线段)
(2)猜想BE与AC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
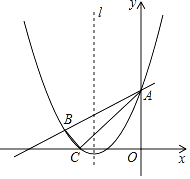
【题目】如图,抛物线![]() 与直线
与直线![]() 分别相交于
分别相交于![]() ,
,![]() 两点,且此抛物线与
两点,且此抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ,连接
,连接![]() ,
,![]() .已知
.已知![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)在抛物线对称轴![]() 上找一点
上找一点![]() ,使
,使![]() 的值最大,并求出这个最大值;
的值最大,并求出这个最大值;
(3)点![]() 为
为![]() 轴右侧抛物线上一动点,连接
轴右侧抛物线上一动点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,问:是否存在点
,问:是否存在点![]() 使得以
使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
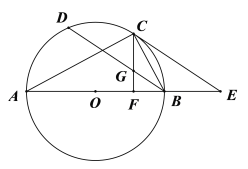
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点C在
,点C在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点C作
,过点C作![]() 于点F,交
于点F,交![]() 于点G,过C作
于点G,过C作![]() 交
交![]() 的延长线于点E.
的延长线于点E.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面改善公园环境,现招标建设某全长960米绿化带,![]() 两个工程队的竞标,
两个工程队的竞标,![]() 队平均每天绿化长度是
队平均每天绿化长度是![]() 队的2倍,若由一个工程队单独完成绿化,
队的2倍,若由一个工程队单独完成绿化,![]() 队比
队比![]() 队要多用6天,
队要多用6天,
(1)分别求出![]() 两队平均每天绿化长度.
两队平均每天绿化长度.
(2)若决定由两个工程队共同合作绿化,要求至多5天完成绿化任务,两队都按(1)中的工作效率绿化完2天时,现又多出510米需要绿化,为了不超过5天时限,两队决定从第3天开始,各自都提高工作效率,且![]() 队平均每天绿化长度仍是
队平均每天绿化长度仍是![]() 队的2倍,则
队的2倍,则![]() 队提高工作效率后平均每天至少绿化多少米?
队提高工作效率后平均每天至少绿化多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com