
����Ŀ��������L��y=a��x��x1����x��x2��������a��0����x�ύ�ڵ�A��x1 �� 0����B��x2 �� 0������y�ύ�ڵ�C����x1x2��0��AB=4����ֱ��l��y=��3x+t+2������t��0��ͬʱ������A��Cʱ��t=1��
��1����C����������
��2�����A��B�����꼰L�Ķ������ꣻ
��3������ͼ2 ��ʾ��ƽ��ֱ������ϵ�У�����L�Ĵ���ͼ��
��4����L����ƽ��t����λ���ȣ�ƽ�ƺ�y��x����������ֵ�ͼ���ΪG����ֱ��l��G�й����㣬ֱ��д��t��ȡֵ��Χ��
���𰸡�
��1����0,3��
��2���⣺��y=0ʱ����3x+3=0�����x1=1����A��1��0����
�ɵ�A��x1��0����B��x2��0������x1x2��0��AB=4��
��1��x2=4�����x2=��3����B����3��0����
L��y=a��x��1����x+3������C��0��3���������L����a=��1��
��L�Ľ���ʽΪy=����x��1����x+3����
��y=����x+1��2+4
��L�Ķ�������Ϊ����1��4����
��3���⣺����ͼ����ͼ

��4���⣺L����ƽ��t����λ�Ľ���ʽΪy=����x+1��t��2+4��
a=��1��0����x��t��1ʱ��y��x�����������
��ֱ��l��G�й�����ʱ�����е�x=��1+tʱ��G��ֱ��l���Ϸ���
������t��1+1��t��2+4�ݩ�3��t��1��+t+2��
���t�� ![]() ��
��
���������⣺��1��ֱ�ߵĽ���ʽΪy=��3x+3��
��x=0ʱ��y=3����C������Ϊ��0��3����
���Դ��ǣ���0��3����


 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ���и���![]() ����
����![]() ��1����������1�������
��1����������1����λ����![]() �������ŵ�2����������2����λ����
�������ŵ�2����������2����λ����![]() ����3����������1����λ����4����������3����λ����5������������1����λ����6����������4����λ�����������˹���������ȥ����P��200����������
����3����������1����λ����4����������3����λ����5������������1����λ����6����������4����λ�����������˹���������ȥ����P��200����������![]() �������ǣ� ��
�������ǣ� ��

A. (51,100)B. (50,100)C. (-50,100)D. (-51,100)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijӪҵ�����ֻ�����ҵ�������µ��Żݣ�
�Żݹ���
���û��ֻ��˻�ԭ�л��Ѳ��ܵ���240Ԫ��
�ڰ���ҵ��ʱ�����ȴ��ֻ��˻���һ���Կ۳�240Ԫ��������240Ԫ��Ϊ300Ԫ���ѣ�Ȼ����300Ԫ���ѷ�12�Σ���ÿ�µ�15�ŵȶ�����ֻ��˻���
��ÿ��1�Ŵ��ֻ��˻��п۳�����49Ԫ�����²��ٿ۳������κη��ã�
��ÿ��1���ֻ��˻��Ļ��������Կ۳�49Ԫʱ����ΪǷ�ѣ����²��ٷ����ȶ�Ļ��ѣ�
С�����ֻ��˻���ԭ�л���400Ԫ�������������Ż�ҵ����С�����ֻ��˻���ÿ����ĩ�Ļ��������y��Ԫ��������Ϊx����������
��1��ÿ���µȶ���Ļ�����Ԫ����2����ĩ�Ļ��������Ԫ��
��2����y����x�ĺ�����ϵʽ��
��3���������ѣ�С�����ֻ��ڼ����»�Ƿ�ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��EF��AD����1=��2����BAC=70�㣬���AGD�Ķ�����
�⣺��EF��AD��
���2= �� ��
�֡ߡ�1=��2��
���1=��3��
��AB�� �� ��
���BAC+ =180�㣨 ��
�ߡ�BAC=70�㣬���AGD= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
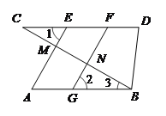
����Ŀ����֪����ͼ��AE��BC��M��FG��BC��N����1����2
��1����֤��AB��CD����2������D����3��50�㣬��CBD��70�㣬���C�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����һ�ڼ���֯ѧ��������Σ������������45���Ŀͳ���������ǡ�������������������60���Ŀͳ���������һ����������30����λ��
(1)��������ε�ѧ�������Ƕ��٣�����45���Ŀͳ����������
(2)��֪45���Ŀͳ�ÿ�����250Ԫ��60���Ŀͳ�ÿ�����300Ԫ��Ϊ��ʡ��𣬲��ұ�֤ÿ��ѧ��������������ͬʱ�������ֿͳ���ʹ��������ȵ���45���Ŀͳ���һ������45���Ŀͳ���60���Ŀͳ��ֱ������������ʹ��������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ô������ȥ������һ�仰������磬�����г�����Խ��Խ�����ǵ�ϲ��������Ʒ�Ƶ�ɽ�����г����Ͷ���г���˳�糵�о�Ӫ��A�ͳ�2015��6�·������ܶ�Ϊ3.2��Ԫ��2016�꾭������������A�ͳ�ÿ�����ۼ۱�2015������400Ԫ����2016��6�·���2015��6�·�������A�ͳ�������ͬ����2016��6�·�A�ͳ������ܶ��2015��6�·������ܶ�����25%.
(1)��2016��6�·�A�ͳ�ÿ�����ۼ�Ϊ����Ԫ(���з��̵ķ������)��
(2)�ó��мƻ�2016��7�·��½�һ��A�ͳ���B�ͳ���50������B�ͳ��Ľ�������������A�ͳ�������������A��B�����ͺų��Ľ��������ۼ۸����±���
A�ͳ� | B�ͳ� | |
�����۸�/(Ԫ/��) | 1100 | 1400 |
���ۼ۸�/(Ԫ/��) | 2016������ۼ۸� | 2400 |
Ӧ��ν�������ʹ������������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʢ����ɫ�߲ˣ���������һ����ɫ�߲ˣ������г���ֱ�����ۣ�ÿ������Ϊ800Ԫ�����ּӹ����ۣ�ÿ������ɴ�2000Ԫ�������ӹ������ۣ�ÿ����������2500Ԫ������һ��ũ���̹�˾�ɹ������߲����ɶ��������ۣ����������о��ӹ�����Ҫ30�������ɣ����������дּӹ�����Ҫ20�������ɣ���֪ÿ�쵥���ּӹ��ȵ������ӹ�������10�֣�
��1���������ũ���̹�˾�ɹ������߲˹����ٶ֣�
��2���������ּӹ���ʽ����ͬʱ�����ܼ����������ƣ���˾������24���ڽ������߲�ȫ�����ۻ�ӹ���ϣ�Ϊ�˸ù�˾���������ֿ��з�����
����һ�����߲�ȫ�����дּӹ���
�������������ܶ�Ķ��߲˽��о��ӹ���û�����ü����мӹ����߲ˣ����г���ֱ�����ۣ�
���������������߲˽��о��ӹ��������߲˽��дּӹ�����ǡ��24����ɣ�����Ϊѡ�����ַ���������ࣿ��ͨ������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com