
【题目】如图,长方形ABCD的边BC在直线l上,AD=5,AB=3,P为直线l上的点,且△ADP是腰长为5的等腰三角形,则BP=_____.

【答案】2.5或1或9或4.
【解析】
根据等腰三角形的性质,分为三种情况,画出图形,再根据勾股定理求出即可.
解:∵长方形ABCD的边BC在直线l上,AD=5,AB=3,
∴BC=AD=5,AB=DC=3,∠ABC=∠BCD=90°,
①如图1,作AD的垂直平分线EF交BC于P1,连接AP1,DP1,
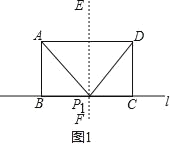
此时AP1=DP1,△ADP1是等腰三角形,BP1=CP1=![]() BC=2.5;
BC=2.5;
②如图2,以D为圆心,以AD为半径作圆,交直线l于P2,P3,
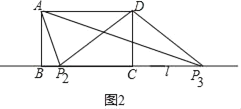
此时△ADP2和△ADP3是等腰三角形,
DP2=DP3=AD=5,
由勾股定理得:CP2=![]() =4,CP3=
=4,CP3=![]() =4,
=4,
∴BP2=5﹣4=1,BP3=5+4=9;
③如图3,以A为圆心,以AD为半径作圆,交直线l于P4,P5,
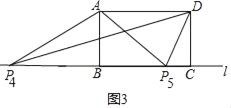
此时△ADP4和△ADP5是等腰三角形,
AP4=AP5=AD=5,
由勾股定理得:BP4=![]() =4,CP′=
=4,CP′=![]() =4,
=4,
即BP的长是2.5或1或9或4;
故答案为:2.5或1或9或4.


科目:初中数学 来源: 题型:
【题目】儿童节期间,某公园游戏场举行一场活动.有一种游戏的规则是:在一个装有8个红球和若干白球(每个球除颜色外,其他都相同)的袋中,随机摸一个球,摸到一个红球就得到一个海宝玩具.已知参加这种游戏的儿童有40 000人,公园游戏场发放海宝玩具8 000个.
(1)求参加此次活动得到海宝玩具的频率?
(2)请你估计袋中白球的数量接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
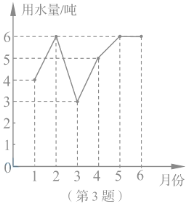
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 经过正方形
经过正方形![]() 的顶点
的顶点![]() ,先分别过此正方形的顶点
,先分别过此正方形的顶点![]() 、
、![]() 作
作![]() 于点
于点![]() 、
、![]() 于点
于点![]() .然后再以正方形对角线的交点
.然后再以正方形对角线的交点![]() 为端点,引两条相互垂直的射线分别与
为端点,引两条相互垂直的射线分别与![]() ,
,![]() 交于
交于![]() ,
,![]() 两点.若
两点.若![]() ,
,![]() ,则线段
,则线段![]() 长度的最小值是___.
长度的最小值是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
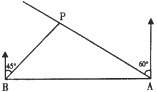
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
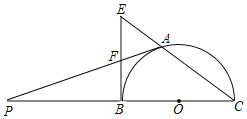
【题目】如图,BC是半⊙O的直径,A是⊙O上一点,过点的切线交CB的延长线于点P,过点B的切线交CA的延长线于点E,AP与BE相交于点F.
(1)求证:BF=EF;
(2)若AF=![]() ,半⊙O的半径为2,求PA的长度.
,半⊙O的半径为2,求PA的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC与△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=BC=4,AD=DE,点F是BE的中点,连接DF,CF.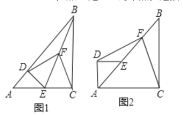
(1)如图1,当点D在AB上,且点E是AC的中点时,求CF的长.
(2)如图1,若点D落在AB上,点E落在AC上,证明:DF⊥CF.
(3)如图2,当AD⊥AC,且E点落在AC上时,判断DF与CF之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长10 dm,宽6 dm矩形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖方盒.
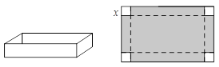
(1) 无盖方盒盒底的长为______dm,宽为_____dm(用含x的式子表示)
(2) 若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com