
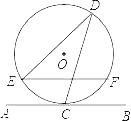
【题目】如图,直线AB与半径为4的⊙O相切于点C,点D在⊙O上,连接CD,DE,且∠EDC=30°,弦EF∥AB,则EF的长为_____.
科目:初中数学 来源: 题型:
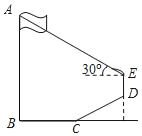
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
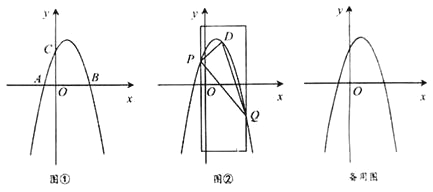
【题目】如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D 的坐标;
,求△DPQ面积的最大值,并求此时点D 的坐标;
②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.
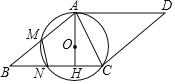
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行革命传统教育,红旗中学开展了“清明节祭扫”活动.全校学生从学校同时出发,步行![]() 米到达烈士纪念馆.学校要求九
米到达烈士纪念馆.学校要求九![]() 班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的
班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的![]() 倍,结果比其他班提前
倍,结果比其他班提前![]() 分钟到达.分别求九(1)班、其他班步行的平均速度.
分钟到达.分别求九(1)班、其他班步行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在运动会前夕,光明中学都会购买篮球、足球作为奖品.若购买6个篮球和8个足球共花费1700元,且购买一个篮球比购买一个足球多花50元.
(1)求购买一个篮球,一个足球各需多少元;
(2)今年学校计划购买这种篮球和足球共10个,恰逢商场在促销活动,篮球打九折,足球打八五折,若此次购买两种球的总费用不超过1150元,则最多可购买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
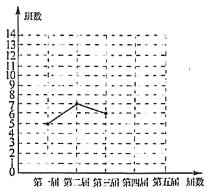
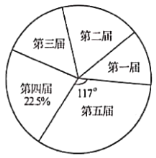
(1)五届艺术节共有________个班级表演这些节日,班数的中位数为________,在扇形统计图中,第四届班级数的扇形圆心角的度数为________;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示).利用树状图或表格求出该班选择
表示).利用树状图或表格求出该班选择![]() 和
和![]() 两项的概率.
两项的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下叙述中,其中正确的有_________(请写出所有正确叙述的序号)
(1)若等腰三角形的一个外角为![]() ,则它的底角为
,则它的底角为![]()
(2)“赵爽弦图”是由于四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示)。小亮同学随机地在大正方形及其内部区域投针,若直角三角形的两条直角边的长分别是2和1,则针扎到小正方形(阴影)区域的概率是![]()
(3)已知关于![]() 的方程
的方程![]() 的解是正数,则
的解是正数,则![]() ;
;
(4)已知正比例函数![]() 反比例函数
反比例函数![]() 由
由![]() 构造一个新函数
构造一个新函数![]() 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).则它有下列一些性质: ①该函数的图象是中心对称图形;②当
其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).则它有下列一些性质: ①该函数的图象是中心对称图形;②当![]() 时,该函数在
时,该函数在![]() 时取得最大值-2;③
时取得最大值-2;③![]() 的值不可能为1;
的值不可能为1;
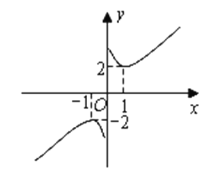
查看答案和解析>>
科目:初中数学 来源: 题型:
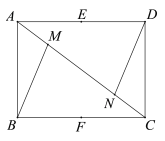
【题目】如图,在矩形ABCD中,AB=3,BC=4.M、N在对角线AC上,且AM=CN,E、F分别是AD、BC的中点.
(1)求证:△ABM≌△CDN;
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com