
【题目】为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台价格,月处理污水量极消耗费如下表:

经预算,该企业购买设备的资金不高于105万元.
⑴ 请你为企业设计几种购买方案.
⑵ 若企业每月产生污水2040吨,为了节约资金,应选那种方案?
【答案】(1)有三种购买方案:方案一:不买A型,买B型10台,方案二,买A型1台,B型9台,方案三,买A型2台,B型8台;(2)为了节约资金应购买A型1台,B型9台,即方案二.
【解析】
(1)设购买污水处理设备A型x台,则B型(10-x)台,列出不等式求解即可,x的值取正整数;
(2)根据企业每月产生的污水量为2040吨,列出不等式求解,再根据x的值选出最佳方案.
解:(1)设购买污水处理设备A型x台,则B型(10-x)台,根据题意得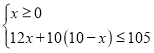 ,
,
解得0≤x≤![]() ,
,
∵x为整数,
∴x可取0,1,2,
当x=0时,10-x=10,
当x=1,时10-x=9,
当x=2,时10-x=8,
即有三种购买方案:
方案一:不买A型,买B型10台,
方案二,买A型1台,B型9台,
方案三,买A型2台,B型8台;
(2)由240x+200(10-x)≥2040
解得x≥1
由(1)得1≤x≤![]()
故x=1或x=2
当x=1时,购买资金12×1+10×9=102(万元)
当x=2时,购买资金12×2+10×8=104(万元)
∵104>102
∴为了节约资金应购买A型1台,B型9台,即方案二.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;

(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置教师办公桌椅A、B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
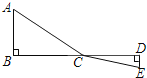
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰直角三角形,AB=AC,AD是斜边的中线,E、F分别是AB、AC边上的点且DE⊥DF.

(1)求证:△AED≌△CFD;
(2)若BE=8,CF=6,求△DEF的面积;
(3)若AB=a,AE=x,请用含x,a的代数式表示△DEF的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为【 】

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com