
【题目】如图,![]() 、
、![]() 是以
是以![]() 为直径的半圆的两条切线,
为直径的半圆的两条切线,![]() 与半圆交于点
与半圆交于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(1)若弧AE的度数为140,求![]() 的度数;
的度数;
(2)求证: ![]() .
.

【答案】(1)∠D=70°,
(2)见详解.
【解析】
(1)连接OE,利用切线证明∠DBA=∠CAB=90°,根据已知得∠AOE=140°,在直角三角形ABD中即可解题;(2)利用同角的余角相等证明∠CEA=∠FEB, ∠CAE=∠EBA即可证明三角形相似.
解:(1)设圆的圆心为点O,连接OE(作图略),
∵![]() 、
、![]() 是以
是以![]() 为直径的半圆的两条切线,
为直径的半圆的两条切线,
∴∠DBA=∠CAB=90°,
∵弧AE的度数为140,即∠AOE=140°,
∵OA=OE,
∴∠EAO=20°,
在直角三角形ABD中,∠D=70°,
(2)∵AB为直径,
∴∠AEB=90°,(直径所对圆周角是90°)
∵![]() ,
,
∴∠CEF=90°,
∴∠CEA=∠FEB(同角的余角相等)
又∵∠CAE+∠EAF=∠EBA+∠EAF
∴∠CAE=∠EBA(同角的余角相等)
∴![]() (有两个角对应相等的三角形是相似三角形)
(有两个角对应相等的三角形是相似三角形)


科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
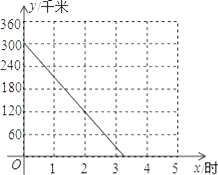
【题目】A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
(1)求y关于x的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为s(千米).请直接写出s关于x的表达式;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为a(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度a.在下图中画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)以下列正方形网络的交点为顶点,分别画出两个相似比不为1的相似三角形,使它们:①都是直角三角形;②都是锐角三角形;③都是钝角三角形.
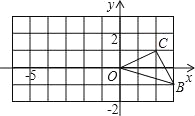
(2)如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).
①以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
②分别写出B、C两点的对应点B′、C′的坐标;
③如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017湖北省鄂州市)小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上.
(1)求树DE的高度;
(2)求食堂MN的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是矗立在高速公路地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,求警示牌CD的高度.(参考数据:![]() =1.41,
=1.41,![]() =1.73).
=1.73).
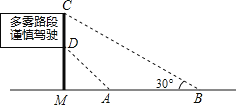
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有A、B两个观测站,C离海岸线l的距离(即CD的长)为2,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则AB的长( )
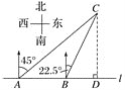
A. 2 km B. (2+![]() )km C. (4-2
)km C. (4-2![]() ) km D. (4-
) km D. (4-![]() ) km
) km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com