
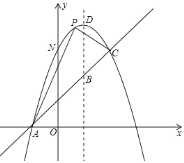
����Ŀ����ͼ����֪������y����x2+bx+c��һֱ���ཻ��A����1��0����C��2��3�����㣬��y�ύ�ڵ�N���䶥��ΪD��
��1��������ֱ��AC�ĺ�����ϵʽ��
��2���������ߵĶԳ�����ֱ��AC�ཻ�ڵ�B��EΪֱ��AC�ϵ�����һ�㣬����E��EF��BD���������ڵ�F����B��D��E��FΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ����E�����ꣻ�����ܣ���˵�����ɣ�
��3����P����������λ��ֱ��AC�Ϸ���һ�����㣬ֱ��д����APC����������ֵ����ʱ��P�����꣮
���𰸡���1��y����x2+2x+3��y��x+1����2�����ڣ����������ĵ�E������Ϊ��0��1������![]() ��
��![]() ����
����![]() ��
��![]() ������3��S��APC�����ֵΪ
������3��S��APC�����ֵΪ![]() ����ʱ��P������Ϊ��
����ʱ��P������Ϊ��![]() ��
��![]() ����
����
��������
��1�����ݵ�A��B�����꣬���ô���ϵ�����������������ֱ��AC�ĺ�����ϵʽ��
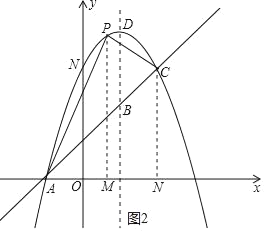
��2�������䷽����һ�κ���ͼ���ϵ�������������������B��D�����꣬���E������Ϊ��x��x+1�����ֵ�E���߶�AC�ϼ���E���߶�AC����CA���ӳ���������������ǣ�������E���߶�AC��ʱ����F�ڵ�E�Ϸ�����BD�ij���ϵ�E������ɵó���F������Ϊ��x��x+3���������ö��κ���ͼ���ϵ���������������x��ֵ�������ɵó���E�����ꣻ������E���߶�AC����CA���ӳ�����ʱ����F�ڵ�E�·�����BD�ij���ϵ�E������ɵó���F������Ϊ��x��x��1���������ö��κ���ͼ���ϵ���������������x��ֵ�������ɵó���E�����꣮���ϣ����ʵý⣻
��3������P��PM��x�ᣬ����Ϊ��M������C��CN��x�ᣬ����ΪN�����P������Ϊ��x����x2+2x+3������1��x��2�������M������Ϊ��x��0������ϵ�A��C�����꼰S��APC��S��APM+S����PMNC��S��ACN���ɵó�S��APC����x�ĺ�����ϵʽ�������ö��κ��������ʼ��ɽ����ֵ���⣮
�⣺��1����A����1��0����C��2��3������y����x2+bx+c���ã�
![]() ����ã�
����ã�![]() ��
��
�������ߵĺ�����ϵʽΪy����x2+2x+3��
��ֱ��AC�ĺ�����ϵʽΪy��kx+a��k��0����
��A����1��0����C��2��3������y��kx+a���ã�
$![]() $����ã�
$����ã�![]() ��
��
��ֱ��AC�ĺ�����ϵʽΪy��x+1��
��2����y����x2+2x+3������x��1��2+4��
���D��������1��4����
��x��1ʱ��y��x+1��2��
���B��������1��2����
���E��������x��x+1����
������������ǣ���ͼ1����
������E���߶�AC��ʱ����F�ڵ�E�Ϸ���
���F��������x��x+3����
�ߵ�F���������ϣ�
��x+3����x2+2x+3��
��ã�x1��0��x2��1����ȥ����
���E��������0��1����
������E���߶�AC����CA���ӳ�����ʱ����F�ڵ�E�·���
���F��������x��x��1����
�ߵ�F���������ϣ�
��x��1����x2+2x+3��
��ã�![]() ��
��
���E��������![]() ����
����![]() ��
��![]() ����
����
���ϣ����������ĵ�E������Ϊ��0��1������![]() ����
����![]() ��
��![]() ����
����
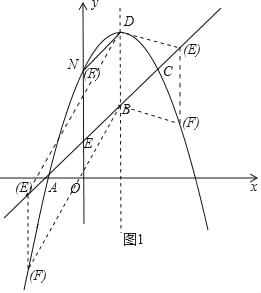
��3������P��PM��x�ᣬ����Ϊ��M������C��CN��x�ᣬ����ΪN����ͼ2��ʾ��
���P��������x����x2+2x+3������1��x��2�������M��������x��0����
�ߵ�A������Ϊ����1��0������C������Ϊ��2��3����
��AM��x+1��MN��2��x��PM����x2+2x+3��CN��3��AN��3��
��S��APC��S��APM+S����PMNC��S��ACN��
![]()
![]()
![]() ��
��
![]()
�൱x��![]() ʱ��S��APCȡ�����ֵ�����ֵΪ
ʱ��S��APCȡ�����ֵ�����ֵΪ![]() ����ʱ��P������Ϊ��
����ʱ��P������Ϊ��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С�ϲμ���![]() �ܵ�5�ڼ�ѵ��ÿ�ڼ�ѵ�����н��в��ԣ��������ǵļ�ѵʱ�䡢���Գɼ����Ƴ���������ͳ��ͼ��
�ܵ�5�ڼ�ѵ��ÿ�ڼ�ѵ�����н��в��ԣ��������ǵļ�ѵʱ�䡢���Գɼ����Ƴ���������ͳ��ͼ��
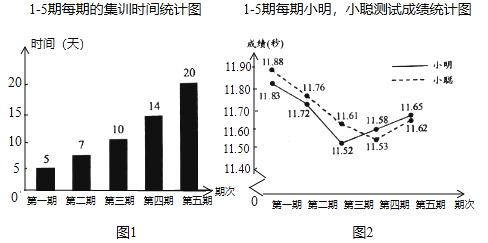
����ͼ����Ϣ������������⣺
��1����5�ڵļ�ѵ���ж����죿С��5�β��Ե�ƽ���ɼ��Ƕ��٣�
��2������ͳ�����ݣ���������˶���ʵ�ʣ��Ӽ�ѵʱ��Ͳ��Գɼ��������棬˵˵����뷨.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У���P��BC����һ���㣨�����B��C�غϣ�������AP��������PD��ʹ��APD=60�㣬PD��AC�ڵ�D����֪AB=a����CD=y��BP=x����y��x������ϵ�Ĵ���ͼ���ǣ�������

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ǽ�����ABCD�Ե�OΪ���İ�˳ʱ�뷽��ֱ���ת90�㣬180�㣬270����γɵ�ͼ�Σ�����BAD=60�㣬AB=2����ͼ����Ӱ���ֵ����Ϊ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
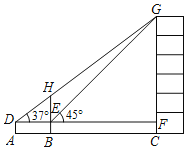
����Ŀ����ͼ��ij��ѧ��ȤС��Ϊ����һ�ù���BH�ͽ�ѧ¥CG�ĸߣ�����A���ø�1.5�IJ���Dz�ù�������H�����ǡ�HDEΪ37�㣬��ʱ��ѧ¥����Gǡ��������DH�ϣ�����ǰ��8����B�����ֲ�ý�ѧ¥����G�����ǡ�GEFΪ45�㣬��A��B��C������ͬһˮƽ���ϣ�
��1�������BH�ĸߣ�
��2�������ѧ¥CG�ĸ߶ȣ�
���ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ż��������ƶ��ն˵�Ѹ�ٷ�չ,���ֻ��Ķ�Խ��Խ�ռ�,�����������ϵġ���ͷ�塱Խ��Խ��.ij�о�������ԡ�����ο������ֻ��Ķ����������������ʾ�����(�ʾ����������ͼ��ʾ),�������������Ƴ�ͼ1��ͼ2��ʾ��ͳ��ͼ(��������).�����ͳ��ͼ���ṩ����Ϣ,�����������:

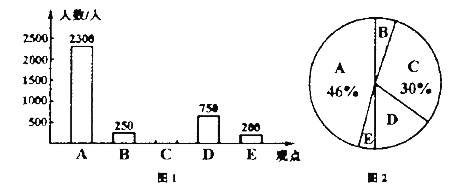
��1�����ν��ܵ���Ĺ��ж�����?
��2���ڽ��ܵ�����˵���,�����ѡ�۵�![]() ��������,��������ͳ��ͼ����������
��������,��������ͳ��ͼ����������
��3��������ͳ��ͼ��,���۵�![]() ����Ӧ��Բ�Ľ�Ϊ���ٶ�?
����Ӧ��Բ�Ľ�Ϊ���ٶ�?
��4���������Ǹ��о��������о�Ա���������ϵ�����,��ֱ��ѡ�۵�![]() ���۵�
���۵�![]() ���۵�
���۵�![]() ���۵�
���۵�![]() �ĵ�����Ա��,ÿ�������ȡ1��,�ٴ���4����,��ѡ2�˽��и�����̸,�����б�������״ͼ����ѡȡ������ǡ����ѡ�۵�
�ĵ�����Ա��,ÿ�������ȡ1��,�ٴ���4����,��ѡ2�˽��и�����̸,�����б�������״ͼ����ѡȡ������ǡ����ѡ�۵�![]() ���۵�
���۵�![]() ���ĸ���.
���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����һ����������ת����ת�̣��������Ϊ4�ȷݣ���ÿһ�ȷݷֱ���ж�Ӧ������2��3��4��5��С����������ת��ת��10�Σ����Ѿ�ת����8�Σ�ÿһ��ֹͣ��С����ָ����ָ���ּ�¼���£�
���� | ��1�� | ��2�� | ��3�� | ��4�� | ��5�� | ��6�� | ��7�� | ��8�� | ��9�� | ��10�� |
���� | 3 | 5 | 2 | 3 | 3 | 4 | 3 | 5 |
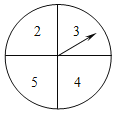
��1����ǰ8�ε�ָ����ָ���ֵ�ƽ������
��2��С����������ת��ת��2�Σ��ж��Ƿ���ܷ�������10�ε�ָ����ָ���ֵ�ƽ������С��3.3���Ҳ�����3.5���Ľ�������п��ܣ����㷢���˽���ĸ��ʣ���д��������̣��������ܣ�˵�����ɣ���ָ��ָ������ȷ���ʱΪ��Чת�Σ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ���Ŀ����Ķ�������ߣ�1�������������ϲ���Ŀ����Ķ���Ŀ�����е��飨ÿ��ѧ������ѡһ����ֻ��ѡһ���Ķ���Ŀ���������ݵ������г�ͳ�Ʊ������Ƴ�����ͳ��ͼ��
�С�Ů����ѡ�������ͳ�Ʊ�
��� | �������ˣ� | Ů�����ˣ� |
��ѧ�� | 12 | 8 |
ʷѧ�� |
| 5 |
��ѧ�� | 6 | 5 |
��ѧ�� | 2 |
|

����������Ϣ�����������
��1��![]() �� ����
�� ����![]() �� ����
�� ����
��2������ͳ��ͼ������ѧ��������Ӧ����Բ�ĽǶ���Ϊ�� ��![]() ��
��
��3����ѡ��ѧ���ѧ���У����ѡȡ����ѧ���μ�ѧУ��ί��֯�ı�������������״ͼ���б��������ѡȡ������ѧ�����������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������5��15�գ����������Ի�����ڱ�����Ļ.Ϊ������ѧ���������Ļ����˽⣬ijѧУ��չ�����֪ʶ�������������Ϊ�˽�����������Ч����ѧУ��ȫУ1200��ѧ���������ȡ100��ѧ������֪ʶ���ԣ���������100�֣��÷־�Ϊ����������������100�˵IJ��Գɼ�������������ͳ��ͼ����
100��ѧ��֪ʶ���Գɼ���Ƶ����
�ɼ� | Ƶ�����ˣ� |
| 10 |
| 15 |
|
|
| 40 |
| 15 |
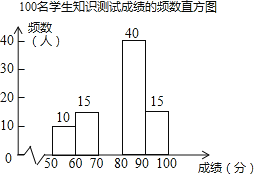
��ͼ���и�������Ϣ�ش��������⣺
��1��![]() ________������ȫ����ֱ��ͼ________��
________������ȫ����ֱ��ͼ________��
��2��С������β����гɼ�Ϊ85�֣�����Ϊ85��һ������100��ѧ��֪ʶ���Գɼ�����λ�������Ҫ˵�����ɣ�
��3�����80�����ϣ�����80�֣�Ϊ���㣬�����ȫУ1200��ѧ���гɼ����������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com