
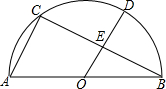
 如图,已知点C,D是半圆$\widehat{AB}$上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:
如图,已知点C,D是半圆$\widehat{AB}$上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①首先根据点C,D是半圆$\widehat{AB}$上的三等分点,求出∠AOC的度数;然后根据圆周角定理,求出∠CBA的度数即可.
②根据三角形的内角和定理,求出∠BEO=90°,即可判断出OD⊥BC.
③首先判断出E是BC的中点,然后判断出OE是△ABC的中位线,即可判断出OE=$\frac{1}{2}$AC.
④菱形的判定方法:四条边都相等的四边形是菱形,据此判断即可.
解答 解:如图,连接CD、AD、CO,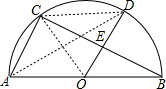 ,
,
∵点C,D是半圆$\widehat{AB}$上的三等分点,
∴∠AOC=∠COD=∠BOD=180°÷3=60°,
∴∠CBA=∠AOC÷2=60°÷2=30°,
即①正确;
∵∠BEO=180°-∠BOD-∠CBA
=180°-60°-30°
=90°
∴OD⊥BC,
即②正确.
∵OB=OC,OD⊥BC,
∴E是BC的中点,
又∵O是AB的中点,
∴OE是△ABC的中位线,
∴OE=$\frac{1}{2}$AC,
即③正确.
∵AC⊥BC,OD⊥BC,
∴AC∥OD,
∵∠DCB=∠BOD÷2=60°÷2=30°,∠CBA=30°
∴∠DCB=∠CBA,
∴CD∥AB,
∴四边形AODC是平行四边形,
∵∠AOC=60°,OA=OC,
∴△AOC是等边三角形,
∴AO=AC,
又∵四边形AODC是平行四边形,
∴AO=OD=DC=CA,
∴四边形AODC是菱形,
即④正确.
综上,可得正确的结论有:①②③④,一共4个.
故选:D.
点评 (1)此题主要考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
(2)此题还考查了圆心角、弧、弦三者的关系,三者的关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.这源于圆的旋转不变性,即:圆绕其圆心旋转任意角度,所得图形与原图形完全重合.
(3)此题还考查了菱形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①四条边都相等的四边形是菱形.②对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱形”).


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
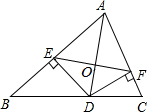 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:| A. | ②③ | B. | ②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$或$\frac{1}{2}$ | B. | 2或3 | C. | $\frac{1}{6}$或1 | D. | 6或1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com