
【题目】据《北京晚报》介绍,自2009年故宫博物院年度接待观众首次突破1000万人次之后,每年接待量持续增长,到2018年突破1700万人次,成为世界上接待量最多的博物馆.特别是随着《我在故宫修文物》、《上新了,故宫》等一批电视文博节目的播出,社会上再次掀起故宫热.于是故宫文创营销人员为开发针对不同年龄群体的文创产品,随机调查了部分参观故宫的观众的年龄,整理并绘制了如下统计图表.
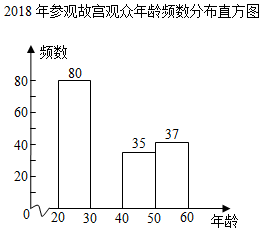
2018年参观故宫观众年龄频数分布表
年龄x/岁 | 频数/人数 | 频率 |
20≤x<30 | 80 | b |
30≤x<40 | a | 0.240 |
40≤x<50 | 35 | 0.175 |
50≤x<60 | 37 | c |
合计 | 200 | 1.000 |
(1)求表中a,b,c的值;
(2)补全频数分布直方图;
(3)从数据上看,年轻观众(20≤x<40)已经成为参观故宫的主要群体.如果今年参观故宫人数达到2000万人次,那么其中年轻观众预计约有 万人次.
科目:初中数学 来源: 题型:
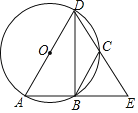
【题目】如图:AD是⊙O的直径,AD=12,点BC在⊙O上,AB、DC的延长线交于点E,且CB=CE,∠BCE=70°,则以下判断中不正确的是( )
A.∠ADE=∠EB.劣弧AB的长为![]() π
π
C.点C为弧BD的中点D.BD平分∠ADE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校拟派一名跳高运动员参加校际比赛,对甲、乙两名同学进行了8次跳高选拔比赛,他们的原始成绩(单位:cm)如下表:
学生/成绩/次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 |
甲 | 169 | 165 | 168 | 169 | 172 | 173 | 169 | 167 |
乙 | 161 | 174 | 172 | 162 | 163 | 172 | 172 | 176 |
两名同学的8次跳高成绩数据分析如下表:
学生/成绩/名称 | 平均数(单位:cm) | 中位数(单位:cm) | 众数(单位:cm) | 方差(单位:cm2) |
甲 | a | b | c | 5.75 |
乙 | 169 | 172 | 172 | 31.25 |
根据图表信息回答下列问题:
(1)a= ,b= ,c= ;
(2)这两名同学中, 的成绩更为稳定;(填甲或乙)
(3)若预测跳高165就可能获得冠军,该校为了获取跳高比赛冠军,你认为应该选择 同学参赛,理由是: ;
(4)若预测跳高170方可夺得冠军,该校为了获取跳高比赛冠军,你认为应该选择 同学参赛,班由是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C地在B地的正东方向,因有大山阻隔,由B地到C地需绕行A地,已知A地位于B地北偏东67°方向,距离B地520km,C地位于A地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求建成高铁后从B地前往C地的路程.(![]() ,结果保留整数)
,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
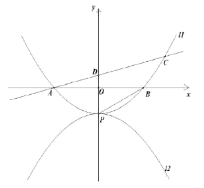
【题目】已知抛物线![]() :
:![]() 的项点为
的项点为![]() ,交
,交![]() 轴于
轴于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧),且
点左侧),且![]() .
.
(1)求抛物线![]() 的函数解析式;
的函数解析式;
(2)过点![]() 的直线交抛物线于点
的直线交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 的面积被
的面积被![]() 轴分为1: 4两个部分,求直线
轴分为1: 4两个部分,求直线![]() 的解析式;
的解析式;
(3)在(2)的情况下,将抛物线![]() 绕点
绕点![]() 逆时针旋转180°得到抛物线
逆时针旋转180°得到抛物线![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,当点
上一点,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 为直角三角形?
为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
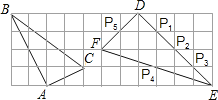
【题目】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明三角形△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似(要求:不写作法与证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系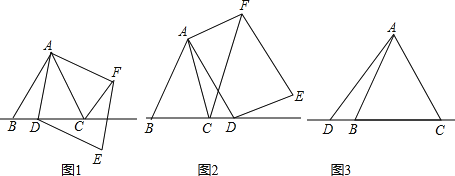
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,抛物线y=a(x+3)(x﹣1)(a>0)与x轴交于A,B两点(点A在点B的左侧).
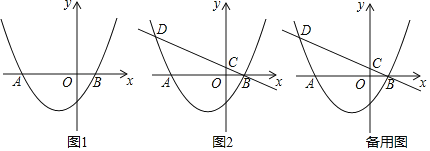
(1)求点A与点B的坐标;
(2)若a=![]() ,点M是抛物线上一动点,若满足∠MAO不大于45°,求点M的横坐标m的取值范围.
,点M是抛物线上一动点,若满足∠MAO不大于45°,求点M的横坐标m的取值范围.
(3)经过点B的直线l:y=kx+b与y轴正半轴交于点C.与抛物线的另一个交点为点D,且CD=4BC.若点P在抛物线对称轴上,点Q在抛物线上,以点B,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
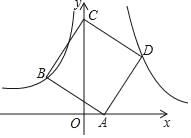
【题目】如图,正方形ABCD的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,点B在双曲线![]() (x<0)上,点D在双曲线
(x<0)上,点D在双曲线![]() (x>0)上,点D的坐标是 (3,3)
(x>0)上,点D的坐标是 (3,3)
(1)求k的值;
(2)求点A和点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com