
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬������y��a��x+3����x��1����a��0����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��
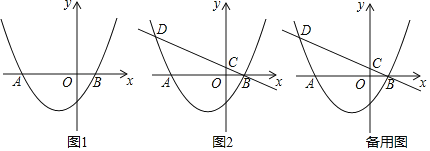
��1�����A���B�����ꣻ
��2����a��![]() ����M����������һ���㣬�������MAO������45�������M�ĺ�����m��ȡֵ��Χ��
����M����������һ���㣬�������MAO������45�������M�ĺ�����m��ȡֵ��Χ��
��3��������B��ֱ��l��y��kx+b��y�������ύ�ڵ�C���������ߵ���һ������Ϊ��D����CD��4BC������P�������߶Գ����ϣ���Q���������ϣ��Ե�B��D��P��QΪ������ı����ܷ��Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��A����3��0����B��1��0������2��M��4��7������2��m��4����3����P������ΪP����1��4����1��![]() ����
����
��������
��1��y��a��x+3����x��1��,��y��0,��x��1��3,�������;
��2���֡�MAO=45��,��M��AO=45���������,�ֱ���⼴��;
��3���ֵ�BD�Ǿ��εı�, BD�Ǿ��εı��������,�ֱ���⼴�ɣ�
��1��y��a��x+3����x��1��,��y��0,��x��1��3,
�ʵ�A��B������ֱ�Ϊ������3��0��,��1��0��;
��2�������ߵı���ʽΪ:y��![]() ��x+3����x��1����,
��x+3����x��1����,
����MAO��45��ʱ,��ͼ��ʾ,��ֱ��AM�ı���ʽΪ:y��x��,
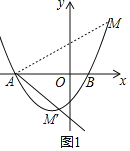
�����٢ڲ����:m��x��4��3����ȥ��3��,�ʵ�M��4,7��;
�ڡ�M��AO��45��ʱ,
ͬ���ɵ�:��M����2,��1��;
��:��2��m��4;
��3���ٵ�BD�Ǿ��εĶԽ���ʱ,��ͼ2��ʾ,
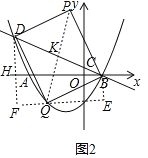
����Q��x���ƽ����EF,����B��BE��EF,����D��DF��EF,
�����ߵı���ʽΪ:y��ax2+2ax��3a,�����ĶԳ���Ϊ:x��1,
�����ߵ�A��B������ֱ�Ϊ:����3,0������1��0��,���P�ĺ�����Ϊ:1,OB��1,
��CD��4BC,���D�ĺ�����Ϊ����4,�ʵ�D����4,5a��,��HD��5a,
�߶�BD���е�K�ĺ�����Ϊ:![]() ,���Q�ĺ�����Ϊ:��2,
,���Q�ĺ�����Ϊ:��2,
���Q����2,��3a��,��HF��BE��3a,
�ߡ�DQF+��BQE��90��,��BQE+��QBE��90��,
���QBE����DQF,
���DFQ�ס�QEB,��![]() ,
,![]() ,���:a��
,���:a��![]() ����ȥ��ֵ��,
����ȥ��ֵ��,
ͬ����PGB�ա�DFQ��AAS��,
��PG��DF��8a��4,�ʵ�P����1,4��;
����ͼ3,��BD�Ǿ��εı�ʱ,
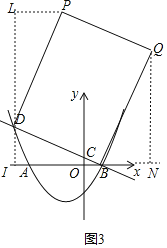
��DI��x��,QN��x��,����P��PL��DI�ڵ�L,
ͬ����PLD�ա�BNQ��AAS��,
��BN��PL��3,
���Q�ĺ�����Ϊ4,���Q��4,21a��,
��QN��DL��21a,ͬ����PLD�ס�DIB,
��![]() ,��
,��![]() ,���:a��
,���:a��![]() ����ȥ��ֵ����
����ȥ��ֵ����
LI��26a��![]() ,�ʵ�P����1,
,�ʵ�P����1, ![]() ��;
��;
����,��P������Ϊ:P����1,4����1, ![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�ˮ�����Ű�����ÿ��2Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��4Ԫ�ļ۸���ۣ�ÿ����۳�100�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�20�Ϊ��֤ÿ�������۳�260��Ű��̾����������ۣ�
��1����������ˮ��ÿ����ۼ۽���xԪ����ÿ����������� ��ú�x�Ĵ���ʽ��ʾ����
��2����������ˮ��Ҫ��ÿ��ӯ��300Ԫ���Ű����轫ÿ����ۼ۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ݡ��������������ܣ���2009��ʹ�����Ժ��ȽӴ������״�ͻ��1000���˴�֮��ÿ��Ӵ���������������2018��ͻ��1700���˴Σ���Ϊ�����ϽӴ������IJ���ݣ��ر������š����ڹʹ���������������ˣ��ʹ�����һ�������IJ���Ŀ�IJ�����������ٴ�����ʹ��ȣ����ǹʹ��Ĵ�Ӫ����ԱΪ������Բ�ͬ����Ⱥ����Ĵ���Ʒ����������˲��ֲι۹ʹ��Ĺ��ڵ����䣬����������������ͳ��ͼ����
2018��ι۹ʹ���������Ƶ���ֲ���
����x/�� | Ƶ��/���� | Ƶ�� |
20��x��30 | 80 | b |
30��x��40 | a | 0.240 |
40��x��50 | 35 | 0.175 |
50��x��60 | 37 | c |
�ϼ� | 200 | 1.000 |
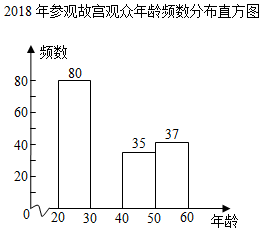
��1�������a��b��c��ֵ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3���������Ͽ���������ڣ�20��x��40���Ѿ���Ϊ�ι۹ʹ�����ҪȺ�壮�������ι۹ʹ������ﵽ2000���˴Σ���ô�����������Ԥ��Լ�� ���˴Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ�˲�����Σ¥��������ֹ��������ʣ����Σ¥¥���������Ų�������Σ¥¥��B�㴦�����Σ¥¥��A������Ϊ60�㣻��¥��B�����ǰ��ǰ��8�����C������C��2�ߵ�D�����Σ¥¥��A������Ϊ30�㣮��������ϲ������ݣ����¥��A�����ĸ߶ȣ���![]() ��1.7����ȷ��1�ף�
��1.7����ȷ��1�ף�
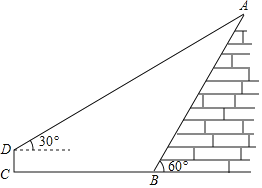
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬������y����![]() x2+bx+c����ԭ�㣬��x�����һ������ΪA����6��0������C�������ߵĶ��㣬�ҡ�C��y�����У���PΪ��C��һ���㣮����DΪPA���е㣬����OD����OD�����ֵ�ǣ�������
x2+bx+c����ԭ�㣬��x�����һ������ΪA����6��0������C�������ߵĶ��㣬�ҡ�C��y�����У���PΪ��C��һ���㣮����DΪPA���е㣬����OD����OD�����ֵ�ǣ�������
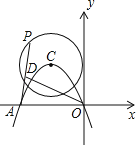
A.![]() B.
B.![]() C.2
C.2![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����¶�![]() ����ͬһˮƽ������һ������
����ͬһˮƽ������һ������![]() ����ѧ��ȤС���ͬѧ��б�µ�
����ѧ��ȤС���ͬѧ��б�µ�![]() ����ø���������
����ø���������![]() ������Ϊ
������Ϊ![]() ��Ȼ�����������¶�Ϊ
��Ȼ�����������¶�Ϊ![]() ��б��
���![]() ������
������![]() �ף����¶�
�ף����¶�![]() ���ֲ�ø���������
���ֲ�ø���������![]() ������Ϊ
������Ϊ![]() �������
�������![]() �ĸ߶ȣ��������ȷ��
�ĸ߶ȣ��������ȷ��![]() �ף��ο����ݣ�
�ף��ο����ݣ� ![]() ��
�� ![]() ��
�� ![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=kx+b��k��0����˫����y=![]() ��m��0�����ڵ�A����
��m��0�����ڵ�A����![]() ��2����B��n����1����
��2����B��n����1����
��1����ֱ����˫���ߵĽ���ʽ��
��2����P��x���ϣ����S��ABP=3�����P�����꣮
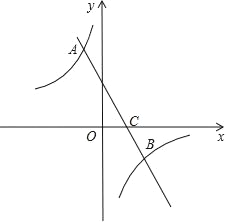
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ϊ�ֻ���ƻ���ֻ���������ϲ����ij�̻�ÿ�ܶ���25000Ԫ����250�Ż�Ϊ�ֻ��Ǻ�150��ƻ���ֻ��ǣ�
��1���̻��ڵ�һ������ʱ��ÿ�Ż�Ϊ�ֻ��ǵ��ۼ۱�ÿ��ƻ���ֻ��ǵ��ۼ۵�2����10Ԫ���������ֻ�����һ��֮��ȫ�����꣬��ӯ��Ϊ5000Ԫ���̻�����ƻ���ֻ��ǵļ۸�ÿ�Ŷ���Ԫ?
��2���̻��ڵڶ�������ʱ���ܵ��������ص�Ӱ�죬ÿ�Ż�Ϊ�ֻ��ǵ��ۼ۱ȵ�һ��ÿ�Ż�Ϊ�ֻ��ǵ��ۼ�����![]() ,����Ϊ�ֻ��ǵ��������ȵ�һ�ܻ�Ϊ�ֻ��ǵ��������½���a%��ÿ��ƻ���ֻ��ǵ��ۼ۱ȵ�һ��ÿ��ƻ���ֻ��ǵ��ۼ��½���a%����ƻ���ֻ������������һ��ƻ���ֻ�����������ͬ������ڶ��ܵ������۶�Ϊ30000Ԫ����a��
,����Ϊ�ֻ��ǵ��������ȵ�һ�ܻ�Ϊ�ֻ��ǵ��������½���a%��ÿ��ƻ���ֻ��ǵ��ۼ۱ȵ�һ��ÿ��ƻ���ֻ��ǵ��ۼ��½���a%����ƻ���ֻ������������һ��ƻ���ֻ�����������ͬ������ڶ��ܵ������۶�Ϊ30000Ԫ����a��![]() ����ֵ��
����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
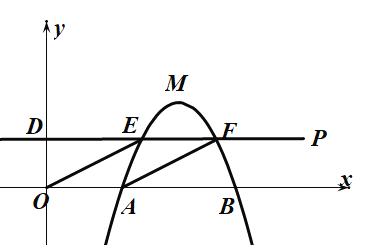
����Ŀ����֪���κ���y����x2+bx+c��ͼ����A��2��0����B��5��0��������D��0��![]() ����y��Ĵ���DP��ͼ����E��F��
����y��Ĵ���DP��ͼ����E��F��
��1����b��c��ֵ�������ߵĶ���M�����ꣻ
��2����֤���ı���OAFE��ƽ���ı��Σ�
��3��������������ƽ�ƵĹ����У������ߵĶ����ΪM�䣬ֱ��DP�������ߵ���ΪE�䣬����OM�䣬OE�䣬��OE��+OM���ֵ��Сʱ��ֱ��OE��Ľ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com