
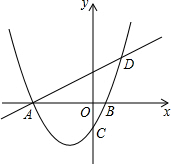
 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,对称轴为直线x=-$\frac{3}{2}$,直线AD交抛物线于点D(2,3).
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,对称轴为直线x=-$\frac{3}{2}$,直线AD交抛物线于点D(2,3).分析 (1)首先根据抛物线的对称轴公式求得b的值,然后代入D的坐标求得c的值,进而得到函数解析式;
(2)在二次函数解析式中令y=0,即可求得函数与x轴交点的横坐标,则A和B的坐标即可求得;
(3)与AC平行,且与抛物线在第三象限只有一个公共点的直线,与抛物线的交点就是M,首先求得AC的解析式,然后设出满足条件的解析式,利用判别式求得.
解答 解:(1)根据对称轴可得-$\frac{b}{2×\frac{1}{2}}$=-$\frac{3}{2}$,
则b=$\frac{3}{2}$,
把(2,3)代入y=$\frac{1}{2}$x2+$\frac{3}{2}$x+c得:2+3+c=3,
解得:c=-2.
则抛物线的解析式是y=$\frac{1}{2}$x2+$\frac{3}{2}$x-2;
(2)令y=0,则$\frac{1}{2}$x2+$\frac{3}{2}$x-2=0,
解得:x=-4或1,
则A的坐标是(-4,0),B的坐标是(1,0);
(3)$\frac{1}{2}$x2+$\frac{3}{2}$x-2=0中令x=0,则y=-2,
则C的坐标是(0,-2).
设AC的解析式是y=kx+b,则$\left\{\begin{array}{l}{-4k+b=0}\\{b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-2}\end{array}\right.$,
则直线AC的解析式是y=-$\frac{1}{2}$x-2.
设与AC平行,且与抛物线在第三象限只有一个公共点的直线的解析式是y=-$\frac{1}{2}$x+b,
则-$\frac{1}{2}$x+b=$\frac{1}{2}$x2+$\frac{3}{2}$x-2,
即x2+4x-(4+2b)=0,
△=16+4(4+2b)=0,
解得:b=-4.
则x=-2.
把x=-2代入y=$\frac{1}{2}$x2+$\frac{3}{2}$x-2得y=-3.
则M的坐标是(-2,-3).
点评 本题考查了待定系数法求函数的解析式,正确根据条件确定M的位置是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
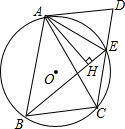 如图,已知四边形ABCD是平行四边形,边CD与⊙O相交于点E,连接AE,BE,∠DAE=∠ABE
如图,已知四边形ABCD是平行四边形,边CD与⊙O相交于点E,连接AE,BE,∠DAE=∠ABE查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-a>y-a | B. | 3-x>3-y | C. | x+2>y+2 | D. | $\frac{x}{3}>\frac{y}{3}$ |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省长宁县双河学区八年级下学期第一次联考数学试卷(解析版) 题型:解答题
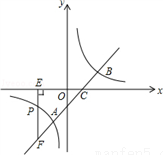
(9分)如图,直线y=x﹣1与反比例函数y=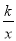 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:单选题
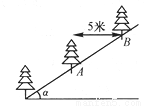
如图,先锋村准备在坡角为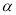 的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A. 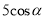 m B.
m B. 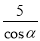 m C.
m C. 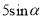 m D.
m D.  m
m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com