
【题目】在正方形![]() 中,
中,![]() 是
是![]() 边上一点,点
边上一点,点![]() 在射线
在射线![]() 上,将线段
上,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() .
.
(1)依题意补全图1;
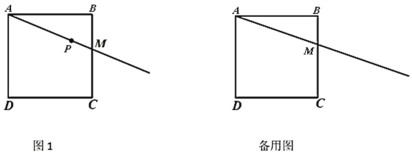
(2)连接![]() ,若点
,若点![]() ,
,![]() ,
,![]() 恰好在同一条直线上,求证:
恰好在同一条直线上,求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据要求画出图形即可;
(2)连接BD,如图2,只要证明△ADQ≌△ABP,∠DPB=90°即可解决问题;
(1)解:补全图形如图1: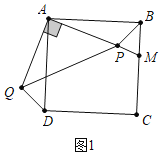
(2)①证明:连接BD,如图2,
∵线段AP绕点A顺时针旋转90°得到线段AQ,
∴AQ=AP,∠QAP=90°,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠1=∠2.
∴△ADQ≌△ABP,
∴DQ=BP,∠Q=∠3,
∵在Rt△QAP中,∠Q+∠QPA=90°,
∴∠BPD=∠3+∠QPA=90°,
∵在Rt△BPD中,DP2+BP2=BD2,
又∵DQ=BP,BD2=2AB2,
∴DP2+DQ2=2AB2.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标为
的坐标为![]() .
.

①把![]() 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的![]() ,画出
,画出![]() ,并写出
,并写出![]() 的坐标;
的坐标;
②以原点![]() 为对称中心,画出
为对称中心,画出![]() 与关于原点
与关于原点![]() 对称的
对称的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
③以原点O为旋转中心,画出把![]() 顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=﹣x2+bx+c经过点A(2,0)、B(0,2).
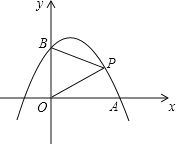
(1)求这条抛物线的解析式;
(2)如图,点P是抛物线上一动点,连接BP,OP,若△BOP是以BO为底边的等腰三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,过
,过![]() 作直线
作直线![]() 交
交![]() 于另一点
于另一点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() 是直径
是直径![]() 上方半圆弧上一动点,
上方半圆弧上一动点,![]() 的半径为2,则
的半径为2,则
①当弦![]() 的长是 时,以
的长是 时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形;
为顶点的四边形是正方形;
②当![]() 的长度是 时,以
的长度是 时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形.
为顶点的四边形是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() )与
)与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,抛物线的对称轴交
,抛物线的对称轴交![]() 轴于点
轴于点![]() ,
,![]() ,并与抛物线的对称轴交于点
,并与抛物线的对称轴交于点![]() .现有下列结论:①
.现有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中所有正确结论的序号是______.
.其中所有正确结论的序号是______.
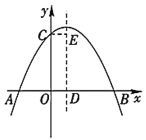
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校一课外活动小组为了了解学生最喜欢的球类运动况,随机抽查了本校九年级的200名学生,调查的结果如图所示,请根据该扇形统计图解答以下问题:
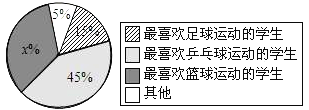
(1)图中![]() 的值是________;
的值是________;
(2)被查的200名生中最喜欢球运动的学生有________人;
(3)若由3名最喜欢篮球运动的学生(记为![]() ),1名最喜欢乒乓球运动的学生(记为
),1名最喜欢乒乓球运动的学生(记为![]() ),1名最喜欢足球运动的学生(记为
),1名最喜欢足球运动的学生(记为![]() )组队外出参加一次联谊活动.欲从中选出2人担任组长(不分正副),列出所有可能情况,并求2人均是最喜欢篮球运动的学生的概率.
)组队外出参加一次联谊活动.欲从中选出2人担任组长(不分正副),列出所有可能情况,并求2人均是最喜欢篮球运动的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
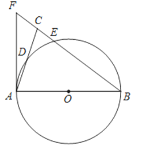
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
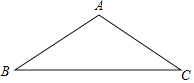
【题目】如图,△ABC.
(1)尺规作图:
①作出底边的中线AD;
②在AB上取点E,使BE=BD;
(2)在(1)的基础上,若AB=AC,∠BAC=120°,求∠ADE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E为对角线AC(不含点A)上任意一点,AB=![]() ;
;
(1)如图1,将△ADE绕点D逆时针旋转90°得到△DCF,连接EF;
①把图形补充完整(无需写画法); ②求![]() 的取值范围;
的取值范围;
(2)如图2,求BE+AE+DE的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com