
【题目】在正方形ABCD中,点E为对角线AC(不含点A)上任意一点,AB=![]() ;
;
(1)如图1,将△ADE绕点D逆时针旋转90°得到△DCF,连接EF;
①把图形补充完整(无需写画法); ②求![]() 的取值范围;
的取值范围;
(2)如图2,求BE+AE+DE的最小值.

【答案】(1)①补图见解析;②![]() ;(2)
;(2)![]()
【解析】
(1)①根据要求画出图形即可;
②首先证明∠ECF=90°,设AE=CF=x,EF2=y,则EC=4x,在Rt△ECF中,利用勾股定理即可解决问题;
(2)如图2中,将△ABE绕点A顺时针旋转60°得到△AFG,连接EG,DF.作FH⊥AD于H.根据两点之间线段最短可得DF≤FG+EG+DE,BE=FG,推出AE+BE+DE的最小值为线段DF的长;
(1)①如图△DCF即为所求;
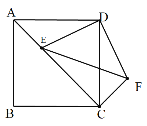
②∵四边形ABCD是正方形,
∴BC=AB=2![]() ,∠B=90°,∠DAE=∠ADC=45°,
,∠B=90°,∠DAE=∠ADC=45°,
∴AC=![]() =
=![]() AB=4,
AB=4,
∵△ADE绕点D逆时针旋转90°得到△DCF,
∴∠DCF=∠DAE=45°,AE=CF,
∴∠ECF=∠ACD+∠DCF=90°,
设AE=CF=x,EF2=y,则EC=4x,
∴y=(4x)2+x2=2x28x+160(0<x≤4).
即y=2(x2)2+8,
∵2>0,
∴x=2时,y有最小值,最小值为8,
当x=4时,y最大值=16,
∴8≤EF2≤16.
(2)如图中,将△ABE绕点A顺时针旋转60°得到△AFG,连接EG,DF.作FH⊥AD于H.
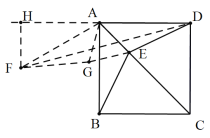
由旋转的性质可知,△AEG是等边三角形,
∴AE=EG,
∵DF≤FG+EG+DE,BE=FG,
∴AE+BE+DE的最小值为线段DF的长.
在Rt△AFH中,∠FAH=30°,AB=![]() =AF,
=AF,
∴FH=![]() AF=
AF=![]() ,AH=
,AH=![]() =
=![]() ,
,
在Rt△DFH中,DF=![]() =
=![]() ,
,
∴BE+AE+ED的最小值为![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 是
是![]() 边上一点,点
边上一点,点![]() 在射线
在射线![]() 上,将线段
上,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() .
.
(1)依题意补全图1;
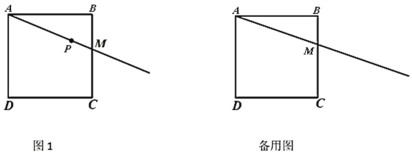
(2)连接![]() ,若点
,若点![]() ,
,![]() ,
,![]() 恰好在同一条直线上,求证:
恰好在同一条直线上,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
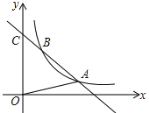
【题目】如图,一次函数的图象与y轴交于C(0,8),且与反比例函数y=![]() (x>0)的图象在第一象限内交于A(3,a),B(1,b)两点.
(x>0)的图象在第一象限内交于A(3,a),B(1,b)两点.
⑴求△AOC的面积;
⑵若![]() =4,求反比例函数和一次函数的解析式.
=4,求反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.

(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙I是△ABC的内切圆,切点分别是D、E、F.
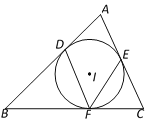
(1)若∠B=50°,∠C=70°,则∠DFE的度数为 ;
(2)若∠DFE=50°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
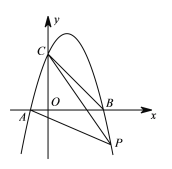
【题目】如图抛物线经![]() 过点
过点![]() ,tan∠CAB=3,且
,tan∠CAB=3,且![]() .
.
(1)求抛物线的解析式及其对称轴;
(2)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为
的面积分为![]() 两部分,求点
两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 为正方形.点
为正方形.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,一次函数
,一次函数![]() 的图象经过点
的图象经过点![]() 和点
和点![]() .
.
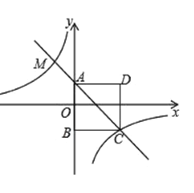
(1)求反比例函数与一次函数的解析式;
(2)写出![]() 的解集;
的解集;
(3)点![]() 是反比例函数图象上的一点,若
是反比例函数图象上的一点,若![]() 的面积恰好等于正方形
的面积恰好等于正方形![]() 的面积,求
的面积,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,一辆小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?______;(填“是”或“否”)请简述你的理由_______.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com