
【题目】如图抛物线经![]() 过点
过点![]() ,tan∠CAB=3,且
,tan∠CAB=3,且![]() .
.
(1)求抛物线的解析式及其对称轴;
(2)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为
的面积分为![]() 两部分,求点
两部分,求点![]() 的坐标.
的坐标.
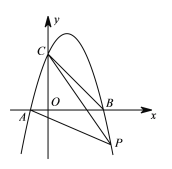
【答案】(1)y=-x2+2x+3;对称轴为:x=1;(2)点P的坐标为(4,-5)或(8,-45).
【解析】
(1)OB=OC,则点B(3,0),则抛物线的表达式为:y=a(x+1)(x-3)=a(x2-2x-3)=ax2-2ax-3a,C点坐标代入可求出a的值,得到抛物线方程,再进行配方即可求出对称轴方程;
(2)根据S△PCB:S△PCA=![]() EB×(yC-yP):
EB×(yC-yP):![]() AE×(yC-yP)=BE:AE求出点E坐标,进而可求出直线PC的解析式,再与抛物线方程联立方程组,求解方程组即可求得点P坐标.
AE×(yC-yP)=BE:AE求出点E坐标,进而可求出直线PC的解析式,再与抛物线方程联立方程组,求解方程组即可求得点P坐标.
(1)∵![]()
∴OA=1,
∵tan∠CAB= ![]() 3
3
∴OC=3
∵OB=OC,
∴点B(3,0),C(0,3)
则抛物线的表达式为:y=a(x+1)(x-3)=a(x2-2x-3)=ax2-2ax-3a,
故-3a=3,解得:a=-1,
故抛物线的表达式为:y=-x2+2x+3=-(x-1)2+4,
函数的对称轴为:x=1;
(2)如图,设直线CP交x轴于点E,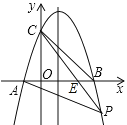
直线CP把四边形CBPA的面积分为3:5两部分,
又∵S△PCB:S△PCA=![]() EB×(yC-yP):
EB×(yC-yP):![]() AE×(yC-yP)=BE:AE,
AE×(yC-yP)=BE:AE,
则BE:AE=3:5或5:3,
∵AB=|-1-3|=4
∴AE=![]() 或
或![]() ,
,
即:点E的坐标为(![]() ,0)或(
,0)或(![]() ,0),
,0),
设直线PC的解析式为:y=kx+b,
将点E(![]() ,0)、C(0,3)的坐标代入一次函数表达式得,
,0)、C(0,3)的坐标代入一次函数表达式得,
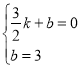 ,解得
,解得![]() ;
;
此时直线CP的表达式为:y=-2x+3;
将点E(![]() ,0)、C(0,3)的坐标代入一次函数表达式得,
,0)、C(0,3)的坐标代入一次函数表达式得,
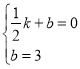 ,解得
,解得![]() ;
;
故直线CP的表达式为: y=-6x+3…②
联立①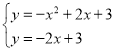 或
或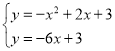
解①得:![]() 或
或 ![]() (不符合题意,舍去))
(不符合题意,舍去))
解②得:![]() 或
或 ![]() (不符合题意,舍去))
(不符合题意,舍去))
所以,点P的坐标为(4,-5)或(8,-45).


科目:初中数学 来源: 题型:
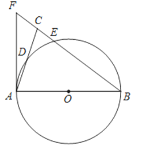
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.

(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E为对角线AC(不含点A)上任意一点,AB=![]() ;
;
(1)如图1,将△ADE绕点D逆时针旋转90°得到△DCF,连接EF;
①把图形补充完整(无需写画法); ②求![]() 的取值范围;
的取值范围;
(2)如图2,求BE+AE+DE的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知实数m,n满足(2m2+n2+1)(2m2+n2-1)=80,试求2m2+n2的值.
解:设2m2+n2=t,则原方程变为(t+1)(t-1)=80,整理得t2-1=80,t2=81,
所以t=土9,因为2m2+n2>0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整休,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
(1)已知实数x、y,满足(2x2+2y2+3)(2x2+2y2-3)=27,求x2+y2的值.
(2)已知Rt△ACB的三边为a、b、c(c为斜边),其中a、b满足(a2+b2)(a2+b2-4)=5,求Rt△ACB外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,以B为圆心,AB为半径作扇形ABC,交对角线BD于点E,过点E作⊙B的切线分别交AD,CD于G,F两点,则图中阴影部分的面积为____.
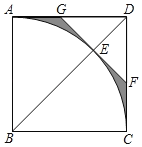
查看答案和解析>>
科目:初中数学 来源: 题型:
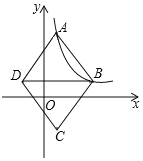
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y![]() (k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴,若菱形ABCD的面积为9.则k的值为____.
(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴,若菱形ABCD的面积为9.则k的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y ax2 bx c(a≠0)的图象,结论:①abc>0;②a - b c<0;③2a b 0;④ax2bxc2018有两个解,其中正确的个数是( )
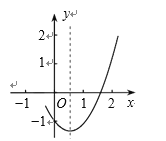
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com