
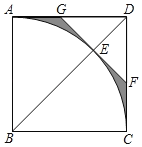
【题目】如图,在边长为2的正方形ABCD中,以B为圆心,AB为半径作扇形ABC,交对角线BD于点E,过点E作⊙B的切线分别交AD,CD于G,F两点,则图中阴影部分的面积为____.
【答案】![]() .
.
【解析】
由四边形ABCD是正方形,且GF是⊙B的切线可证出△DGF是等腰直角三角形,再由正方形的边长可知BE的长,再求出DE的长,继而求出DG的长,再利用正方形面积-扇形面积-三角形面积即可求出阴影部分的面积.
∵四边形ABCD是正方形,
∴∠ABC=∠ADC=90°,∠GDE=∠FDE=45°.
∵GF是⊙B的切线,
∴BD⊥GF,
∴∠DEG=∠DEF=90°,
∴∠DGE=45°,∠DFE=45°,
∴DG=DF,GF=2DE,
∴DG=DF![]() DE.
DE.
∵BD![]() AB=2
AB=2![]() ,
,
∴DE=BD﹣BE=2![]() 2,
2,
∴DG=DF![]() (2
(2![]() 2)=4﹣2
2)=4﹣2![]() ,
,
S阴影=S正方形ABCD﹣S扇形BAC﹣S△DGF
=2×2![]() (4﹣2
(4﹣2![]() )2
)2
=8![]() 8﹣π.
8﹣π.
故答案为:8![]() 8﹣π.
8﹣π.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分9分)如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.

(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙I是△ABC的内切圆,切点分别是D、E、F.
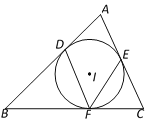
(1)若∠B=50°,∠C=70°,则∠DFE的度数为 ;
(2)若∠DFE=50°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
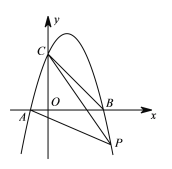
【题目】如图抛物线经![]() 过点
过点![]() ,tan∠CAB=3,且
,tan∠CAB=3,且![]() .
.
(1)求抛物线的解析式及其对称轴;
(2)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为
的面积分为![]() 两部分,求点
两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于不在坐标轴上的任意一点P(x,y),我们把的P'(![]() ,
,![]() )称为点P的“倒影点”.直线y=﹣2x+1上有两点A、B,它们的倒影点A'、B'均在反比例函数y
)称为点P的“倒影点”.直线y=﹣2x+1上有两点A、B,它们的倒影点A'、B'均在反比例函数y![]() 的图象上,若AB
的图象上,若AB![]() ,则k的值为( )
,则k的值为( )
A.![]() B.
B.![]() C.5D.10
C.5D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 为正方形.点
为正方形.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,一次函数
,一次函数![]() 的图象经过点
的图象经过点![]() 和点
和点![]() .
.
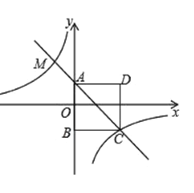
(1)求反比例函数与一次函数的解析式;
(2)写出![]() 的解集;
的解集;
(3)点![]() 是反比例函数图象上的一点,若
是反比例函数图象上的一点,若![]() 的面积恰好等于正方形
的面积恰好等于正方形![]() 的面积,求
的面积,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC切⊙O于点C,AB交⊙O于点D,BC的中点为 E,连接DE.
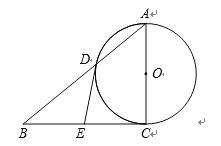
(1)求证:BE DE;
(2)连接EO交⊙O于点 F.填空:
①当∠B __________时,以 D,E,C,O为顶点的四边形是正方形;
②当∠B __________时,以 A,D,F,O为顶点的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com