
【题目】如图,AC是⊙O的直径,BC切⊙O于点C,AB交⊙O于点D,BC的中点为 E,连接DE.
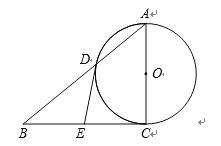
(1)求证:BE DE;
(2)连接EO交⊙O于点 F.填空:
①当∠B __________时,以 D,E,C,O为顶点的四边形是正方形;
②当∠B __________时,以 A,D,F,O为顶点的四边形是菱形.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)由题意根据直角三角形斜边中线的性质即可证明;
(2)①如图2-1中,当∠B=45°时,以D,E,C,O为顶点的四边形是正方形;
②如图2-2中,结论:∠B=45°;利用①结论证明DE=OA,DE∥OA即可.
(1)证明:连接CD,OD,OE.
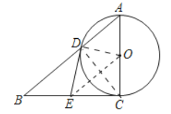
∵AC是直径,
∴∠ADC=∠BDC=90°,
∵BE=EC,
∴DE=CE=BE,
∴BE=DE.
(2)①如图2-1中,当∠B=45°时,以D,E,C,O为顶点的四边形是正方形;
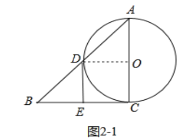
理由:∵BC是⊙O的切线,
∴AC⊥BC,
∴∠ACB=90°,
∵OD=OC,OE=OE,DE=CE,
∴△EOD≌△EOC(SSS),
∴∠EDO=∠ECO=90°,
∵EB=ED,
∴∠B=∠EDB=45°,
∴∠DEC=∠B+∠EDB=90°,
∴四边形DECO是矩形,
∵OD=OC,
∴四边形DECO是正方形.
故答案为:45°.
②如图2-2中,结论:∠B=45°.
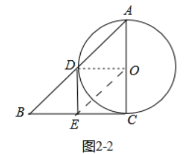
当∠B=45°时,由①可知四边形DECO是正方形.
∴DE∥OC,DE=OC,
∵OC=OA,
∴DE=OA,DE∥OA,
∴四边形ADEO是平行四边形.
故答案为:45°.


科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D是![]() 的中点,AD交BC于点E,若CE=
的中点,AD交BC于点E,若CE=![]() ,BE=
,BE=![]() ,以下结论中:①sin∠ABC=
,以下结论中:①sin∠ABC=![]() ;②AD=
;②AD=![]() ,③S⊙O=
,③S⊙O=![]() π;④OE∥BD.其中正确的共有( )个.
π;④OE∥BD.其中正确的共有( )个.
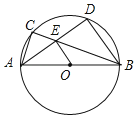
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,以B为圆心,AB为半径作扇形ABC,交对角线BD于点E,过点E作⊙B的切线分别交AD,CD于G,F两点,则图中阴影部分的面积为____.
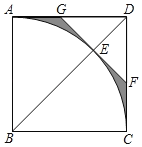
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泗县在省级文明城市创建中,举行“小手拉大手,倡导文明新风尚”的活动中,九年级的5名同学(三男两女)成立了“交通秩序维护”小分队,若从该小分队中任选两名同学进行交通秩序维护,则恰是一男一女的概率是多少?请用树状图或列表法说明所有可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y ax2 bx c(a≠0)的图象,结论:①abc>0;②a - b c<0;③2a b 0;④ax2bxc2018有两个解,其中正确的个数是( )
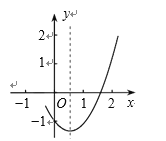
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是( )
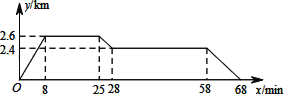
A.食堂离小明家2.4km
B.小明在图书馆呆了20min
C.小明从图书馆回家的平均速度是0.04km/min
D.图书馆在小明家和食堂之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中有![]() ,
,![]() 为坐标原点,
为坐标原点,![]() ,将此三角形绕原点
,将此三角形绕原点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,二次函数
,二次函数![]() 的图象刚好经过
的图象刚好经过![]() 三点.
三点.
(1)求二次函数的解析式及顶点![]() 的坐标;
的坐标;
(2)过定点![]() 的直线
的直线![]() 与二次函数图象相交于
与二次函数图象相交于![]() 两点.
两点.
①若![]() ,求
,求![]() 的值;
的值;
②证明:无论![]() 为何值,
为何值,![]() 恒为直角三角形;
恒为直角三角形;
③当直线![]() 绕着定点
绕着定点![]() 旋转时,
旋转时,![]() 外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
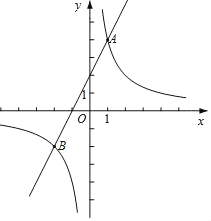
【题目】如图,在平面直角坐标系xOy中,直线y=2x+2与函数y=![]() (k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(1)求k,m的值;
(2)已知点P(a,0),过点P作平行于y轴的直线,交直线y=2x+2于点M,交函数y=![]() (k≠)的图象于点N.
(k≠)的图象于点N.
①当a=2时,求线段MN的长;
②若PM>PN,结合函数的图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线![]() 与直线
与直线![]() 交于两点
交于两点![]() .已知点
.已知点![]() 坐标为
坐标为![]()
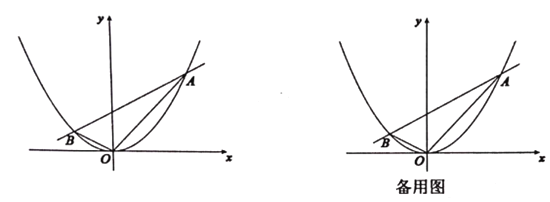
(1)求![]() 点坐标;
点坐标;
(2)求![]() 的面积;
的面积;
(3)将直线![]() 从原点出发向上平移
从原点出发向上平移![]() 个单位,设
个单位,设![]() 为直线平移后其上一点,且满足
为直线平移后其上一点,且满足![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com