
【题目】如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻AB在阳光下的投影BC=2 m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影长时,同时测量出DE在阳光下的投影长为5 m,请你计算DE的长.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.现从点
的中点.现从点![]() 观察线段
观察线段![]() ,当长度为
,当长度为![]() 的线段
的线段![]() (图中的黑粗线)以每秒
(图中的黑粗线)以每秒![]() 个单位长的速度沿线段
个单位长的速度沿线段![]() 从左向右运动时,
从左向右运动时,![]() 将阻挡部分观察视线,在
将阻挡部分观察视线,在![]() 区域内形成盲区.设
区域内形成盲区.设![]() 的左端点从
的左端点从![]() 点开始,运动时间为
点开始,运动时间为![]() 秒
秒![]() .设
.设![]() 区域内的盲区面积为
区域内的盲区面积为![]() (平方单位).
(平方单位).

![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 请简单概括
请简单概括![]() 随
随![]() 的变化而变化的情况.
的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
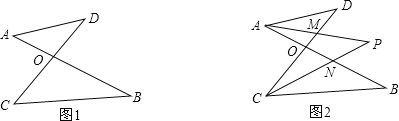
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)图2中,当∠D=40°,∠B=30°度时,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C 是线段 AB 上一点,且△ACD 和△BCE 都是等边三角形,连接 AE、BD 相交于点 O,AE、BD 分别交 CD、CE 于 M、N,连接 MN、OC,则下列所给的结论中:①AE=BD;②CM=CN;③MN∥AB;④∠AOB=120;⑤OC 平分∠AOB.其中结论正确的个数是( )

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 个单位长度的小正方形组成的网格中,按要求画出
个单位长度的小正方形组成的网格中,按要求画出 和
和 ;
;

![]() 把
把![]() 先向右平移
先向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,得到
个单位,得到 ;
;
![]() 以图中的
以图中的![]() 为位似中心,将
为位似中心,将 作位似变换且放大到原来的两倍,得到
作位似变换且放大到原来的两倍,得到 ;
;
![]() 直接回答
直接回答 ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=k(x-1)与一次函数y2=-k(x-3)的图像交于点P,其中k≠0.

(1)求点P的横坐标.
(2)点A(a,y)和点B(b,y)分别在y1和y2的图像上,若a=5,求b的值.
(3)点C(x,m)和点D(x,n)分别在y1和y2的图像上,若m-n>k,当k>0时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个长为4cm,宽为3cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板点A位置的变化为A→Al→A2,其中第二次翻滚被面上一小木块挡住,使木板与桌面成30°的角,则点A滚到A2位置时共走过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2:按上述方法不断操作下去…,经过第2019次操作后得到的折痕D2018E2018,到BC的距离记为h2019:若h1=1,则h2019的值为(____)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1是一个重要公式的几何解释.请你写出这个公式: ;
(2)如图2,已知![]() ,
,![]() ,且
,且![]() 三点共线.
三点共线.
试证明![]() ;
;

(3)勾股定理是几何学中的明珠,千百年来,人们对它的证明趋之若骛,有资料表明,关于勾股定理的证明方法已有500余种.课本中介绍了比较有代表性的赵爽弦图.
伽菲尔德(Garfield,1881年任美国第20届总统)利用图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),请你写出该证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com