
【题目】某校对九年一班50名学生进行长跑项目的测试,根据测试成绩制作了两个统计图.
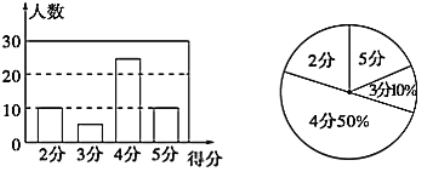
请根据相关信息,解答下列问题:
(1)本次测试的学生中,得3分的学生有________人,得4分的学生有________人;
(2)求这50个数据的平均数、众数和中位数.
科目:初中数学 来源: 题型:
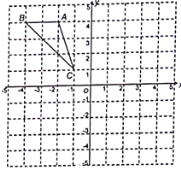
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)请画出![]() 向下平移6个单位长度后得到的
向下平移6个单位长度后得到的![]() ;
;
(2)请画出![]() 绕原点
绕原点![]() 顺时针旋转
顺时针旋转![]() 后得到的
后得到的![]() ;
;
(3)求出(2)中点![]() 旋转到
旋转到![]() 点所经过的路径长(结果保留根号和
点所经过的路径长(结果保留根号和![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圆,过点
的外接圆,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
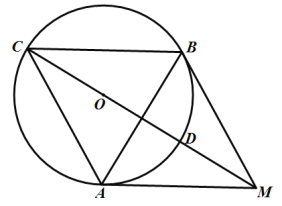
(1)求证:![]() ;
;
(2)填空:
①若![]() ,
,![]() ________;
________;
②连接![]() ,当
,当![]() 的度数为________时,四边形
的度数为________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
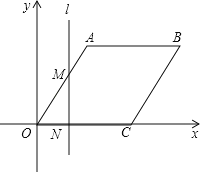
【题目】如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)求A、B两点的坐标;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
(3)在题(2)的条件下,是否存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4?如果存在,请求出t的取值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园音乐之声“结束后,王老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如下频数直方图和扇形统计图:
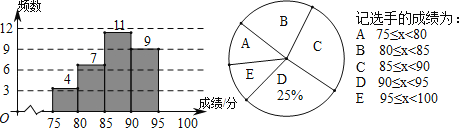
(1)求本次比赛参赛选手总人数,并补全频数直方图;
(2)求扇形统计图中扇形E的圆心角度数;
(3)成绩在E区域的选手中,男生比女生多一人,从中随机选取两人,求恰好选中两名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
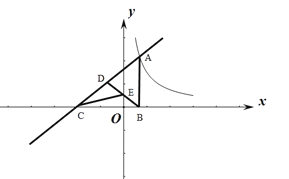
【题目】已知直线y=2x+b与反比例函数y=![]() 的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E.
的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E.
(1)若k=8,且点A的横坐标为1,求b的值;
(2)已知△BEC的面积为4,则k的值为多少?
(3)在(2)的条件下,已知点E为△ABC的重心,且OE=2,求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售甲、乙两种品牌的投影仪,这两种投影仪的进价和售价如下表所示:
甲 | 乙 | |
进价(元/套) | 3000 | 2400 |
售价(元/套) | 3300 | 2800 |
该公司计划购进两种投影仪若干套,共需66000元,全部销售后可获毛利润9000元.
(1)该公司计划购进甲、乙两种品牌的投影仪各多少套?
(2)通过市场调研,该公司决定在原计划的基础上,减少甲种投影仪的购进数量,增加乙种投影仪的购进数量,已知乙种投影仪增加的数量是甲种投影仪减少的数量的2倍。若用于购进这两种投影仪的总资金不超过75000元,问甲种投影仪购进数量至多减少多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com