
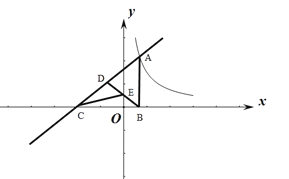
【题目】已知直线y=2x+b与反比例函数y=![]() 的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E.
的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E.
(1)若k=8,且点A的横坐标为1,求b的值;
(2)已知△BEC的面积为4,则k的值为多少?
(3)在(2)的条件下,已知点E为△ABC的重心,且OE=2,求直线AC的解析式.
【答案】(1)b=6;(2)k=8;(3)![]()
【解析】
(1)将点![]() 的横坐标
的横坐标![]() 代入解析式,即可求得
代入解析式,即可求得![]() 点坐标为(1,8),再代入一次函数解析式即可求得
点坐标为(1,8),再代入一次函数解析式即可求得![]() ;
;
(2)过点![]() 作
作![]() 轴与点
轴与点![]() ,
,![]() 交
交![]() 轴于
轴于![]() ,易证
,易证![]() ,再分别设出每个点的坐标,即可表示出
,再分别设出每个点的坐标,即可表示出![]() ,因为点A既在抛物线上也在直线上,通过坐标进行转化化简后,可以求得
,因为点A既在抛物线上也在直线上,通过坐标进行转化化简后,可以求得![]() ;
;
(3)△BEC的面积为4,利用重心的性质:可知DE:BE=1:2,进而可以求得△ABC的面积为12,进而求得BC、AB,过点D作DH![]() AB于H,交
AB于H,交![]() 轴于K,通过平行线分线段成比例,分别可求得DK、KH,即可知A点坐标,代入一次函数解析式,即可求解.
轴于K,通过平行线分线段成比例,分别可求得DK、KH,即可知A点坐标,代入一次函数解析式,即可求解.
解:(1)∵![]() ,则反比例函数解析式为
,则反比例函数解析式为![]() ,将点A的横坐标
,将点A的横坐标![]() 代入解析式,
代入解析式,
解得![]() ,故
,故![]() 点坐标为(1,8),再将点A代入一次函数解析式得
点坐标为(1,8),再将点A代入一次函数解析式得![]() ,
,
解得![]() =6;
=6;
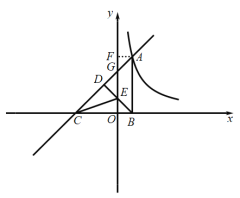
(2)过点![]() 作
作![]() 轴与点
轴与点![]() ,
,![]() 交
交![]() 轴于
轴于![]() ,则有
,则有![]() ,
,
∴![]() ,
,
∵![]() 为直角三角形,且点
为直角三角形,且点![]() 为中点,
为中点,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中 ,
,
∴![]() ,
,
∴![]() ,
,
设点B的坐标为(![]() ,
,![]() ),则A点的坐标为(
),则A点的坐标为(![]() ,
,![]() ),C点的坐标为(
),C点的坐标为(![]() ,
,![]() ),
),
G点坐标为(![]() ,
,![]() ),F点坐标为(
),F点坐标为(![]() ,
,![]() ),
),
∴ ![]() ,
,
而点A也在一次函数图像上,故![]() ,代入上式,整理得:
,代入上式,整理得:
![]() ,即
,即![]() ,而
,而![]() ,
,
故![]() ,即
,即![]() ;
;
(3)∵E为重心,根据重心的性质,
∴DE:BE=1:2,而![]() ,
,
∴![]() ,即
,即![]() ,
,
∵D为AC中点,
∴![]() ,
,
∵![]() ,OE=
,OE=![]() ,
,
∴BC=![]() ,
,
∴![]() , 即AB=
, 即AB=![]() ,
,
过点D作DH![]() AB于点H,交
AB于点H,交![]() 轴于点
轴于点![]() ,
,

则有:![]() ,DH为中位线,
,DH为中位线,
∴![]() , 即
, 即![]() ,
,
求得:![]() ,
,![]() ,
,
即点A坐标为(![]() ,6),再代入
,6),再代入![]() 中,解得:
中,解得:![]() .
.
故直线AC的解析式为:![]() .
.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】在学习函数时,我们经历了“确定函数的表达式利用函数图象研究其性质——运用函数解决问题“的学习过程,在画函数图象时,我们通过列表、描点、连线的方法画出了所学的函数图象
同时,我们也学习过绝对值的意义![]() .
.
结合上面经历的学习过程,现在来解决下面的问题:
在函数y=|kx-1|+b中,当x=0时,y=-2;当x=1时,y=-3.
(1)求这个函数的表达式;
(2)在给出的平面直角坐标系中,请直接画出此函数的图象并写出这个函数的两条性质;
(3)在图中作出函数y=![]() 的图象,结合你所画的函数图象,直接写出不等式|kx-1|+b≤
的图象,结合你所画的函数图象,直接写出不等式|kx-1|+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对九年一班50名学生进行长跑项目的测试,根据测试成绩制作了两个统计图.
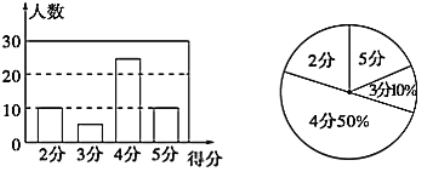
请根据相关信息,解答下列问题:
(1)本次测试的学生中,得3分的学生有________人,得4分的学生有________人;
(2)求这50个数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=3,点P是边AB上的一动点,连接DP,
(1)若将△DAP沿DP折叠,点A落在矩形的对角线上点A处,试求AP的长;
(2)点P运动到某一时刻,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP与PE折叠,点A与点B分别落在点A,B处,若P,A,B三点恰好在同一直线上,且AB=2,试求此时AP的长.
(3)当点P运动到边AB的中点处时,过点P作直线PG交BC于点G,将△DAP与△PBG分别沿DP与PG折叠,点A与点B重合于点F处,请直接写出F到BC的距离.
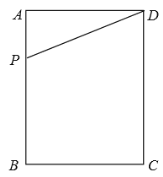
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:
的四个命题:
①当x=0时,y有最小值12;
②n为任意实数,x=3+n时的函数值大于x=3-n时的函数值;
③若n>3,且n是整数,当![]() 时,y的整数值有
时,y的整数值有![]() 个;
个;
④若函数图象过点![]() 和
和![]() ,其中a>0,b>0,则a<b.
,其中a>0,b>0,则a<b.
其中真命题的序号是( )
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
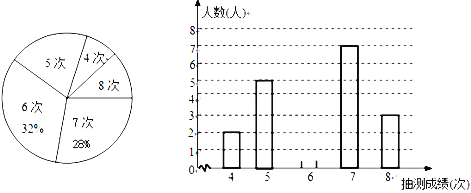
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请将条形图补充完整;
(3)若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第一个等式:![]() ;
;
第二个等式:![]() ;
;
第三个等式:![]() ;
;
第四个等式:![]() ;
;
按上述规律,回答下列问题:
(1)请写出第六个等式:a6= = ;
(2)用含n的代数式表示第n个等式:an= = ;
(3)a1+a2+a3+a4+a5+a6= (得出最简结果);
(4)计算:a1+a2+…+an.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.
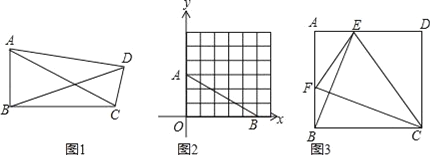
(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年8月.山西龙城将迎来全国第二届青年运动会,盛会将至,整个城市已经进入了全力准备的状态.太职学院足球场作为一个重要比赛场馆.占地面积约24300平方米.总建筑面积4790平方米,设有2476个座位,整体建筑简洁大方,独具特色.2018年3月15日该场馆如期开工,某施工队负责安装该场馆所有座位,在安装完476个座位后,采用新技术,效率比原来提升了![]() .结来比原计划提前4天完成安装任务.求原计划每天安装多少个座位.
.结来比原计划提前4天完成安装任务.求原计划每天安装多少个座位.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com