
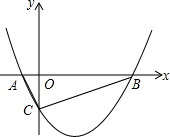
 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴相交于点A和点B,与y轴相交于点C,在抛物线上是否存在点P,使得∠PBO=∠BCO?若存在,求出点P的坐标;若不存在,请说明理由.
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴相交于点A和点B,与y轴相交于点C,在抛物线上是否存在点P,使得∠PBO=∠BCO?若存在,求出点P的坐标;若不存在,请说明理由. 分析 先利用抛物线与x轴的交点问题,通过解方程$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0得到A(-1,0),B(4,0),再求出C(-2,0),接着利用待定系数法求出直线AC的解析式为y=-2x-2,再证明△AOC∽△COB得到∠BCO=∠CAO,所以过B作BP∥AC交抛物线于P,满足∠PBO=∠BCO,然后确定直线与抛物线的交点坐标可确定此时P点坐标;再利用对称性可确定当点P与点C关于直线x=$\frac{3}{2}$对称时,满足∠PBO=∠BCO,易得此时P点坐标为(3,-2).
解答 解:存在.
当y=0时,$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0,解得x1=-1,x2=4,则A(-1,0),B(4,0),
当x=0时,y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2=-2,则C(-2,0),
设直线AC的解析式为y=kx+b,
把A(-1,0),C(0,-2)代入得$\left\{\begin{array}{l}{-k+b=0}\\{b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=-2}\end{array}\right.$,
所以直线AC的解析式为y=-2x-2;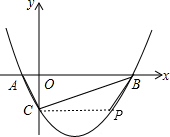
∵$\frac{OC}{OA}$=$\frac{OB}{OC}$,
而∠AOC=∠COB,
∴△AOC∽△COB,
∴∠BCO=∠CAO,
过B作BP∥AC交抛物线于P,则∠PBO=∠CAB,则∠PBO=∠BCO,
设此时BP的解析式为y=-2x+t,
把B(4,0)代入得-8+t=0,解得t=8,
解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-2}\\{y=-2x+8}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-5}\\{y=18}\end{array}\right.$,
∴此时P点坐标为(-5,18);
抛物线的对称轴为直线x=$\frac{3}{2}$,
当点P与点C关于直线x=$\frac{3}{2}$对称时,∠CAO=∠PBO,则∠PBO=∠BCO,
∴此时P点坐标为(3,-2),
综上所述,满足条件的P点坐标为(-5,18)或(3,-2).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了相似三角形的判定与性质.


科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,有下列四个条件:①AB=BE;②DE⊥DC;③∠ADB=90°;④CE⊥DE.如果添加其中一个条件就能使四边形DBCE成为矩形,那么这个条件是①或③或④.
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,有下列四个条件:①AB=BE;②DE⊥DC;③∠ADB=90°;④CE⊥DE.如果添加其中一个条件就能使四边形DBCE成为矩形,那么这个条件是①或③或④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
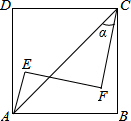 如图,正方形ABCD内有两点E、F满足AE=4,tanα=$\frac{3}{4}$,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为10$\sqrt{2}$.
如图,正方形ABCD内有两点E、F满足AE=4,tanα=$\frac{3}{4}$,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为10$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com