
【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.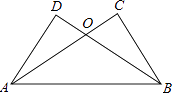
求证:
(1)BC=AD
(2)△OAB是等腰三角形.
【答案】
(1)
证明:∵AC⊥BC,BD⊥AD,
∴∠ADB=∠ACB=90°,
在Rt△ABC和Rt△BAD中,
∵ ![]() ,
,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD,
(2)
证明:∵Rt△ABC≌Rt△BAD, ∴∠CAB=∠DBA,
∴OA=OB,
∴△OAB是等腰三角形.
【解析】(1)根据AC⊥BC,BD⊥AD,得出△ABC与△BAD是直角三角形,再根据AC=BD,AB=BA,得出Rt△ABC≌Rt△BAD,即可证出BC=AD,(2)根据Rt△ABC≌Rt△BAD,得出∠CAB=∠DBA,从而证出OA=OB,△OAB是等腰三角形.
【考点精析】掌握等腰三角形的判定是解答本题的根本,需要知道如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是 时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是 时,它们一定不全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)29×20.18+72×20.18+13×20.18-14×20.18;
(2)1002-992+982-972+…+42-32+22-12.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
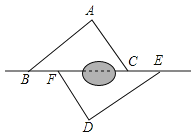
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B= ![]() ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com