
【题目】(1)已知x=![]() -1,求x2+3x-1的值;
-1,求x2+3x-1的值;
(2)若|x-4|+![]() +(z+27)2=0,求
+(z+27)2=0,求![]() +
+![]() -
-![]() 的值;
的值;
(3)已知![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() -1;(2)3;(3)a=±
-1;(2)3;(3)a=±![]() 或a=±2.
或a=±2.
【解析】
(1)直接将已知数据代入求出即可;(2)由于|x-4|+![]() +(z+27)2=0,根据绝对值、平方、算术平方根等非负数的性质即可求出x、y、z的值、然后即可解决问题;(3)
+(z+27)2=0,根据绝对值、平方、算术平方根等非负数的性质即可求出x、y、z的值、然后即可解决问题;(3)
一个数的算术平方根等于它本身的只有0,1,令a2-3=0或1,从而求出答案.
(1)将x=![]() -1代入原式可得:原式=(
-1代入原式可得:原式=(![]() -1)2+3(
-1)2+3(![]() -1)-1=2-2
-1)-1=2-2![]() +1+3
+1+3![]() -3-1=
-3-1=![]() -1;(2)∵|x-4|+
-1;(2)∵|x-4|+![]() +(z+27)2=0,∴x-4=0,y+8=0,z+27=0,∴x=4,y=-8,z=-27,将三个数代入原式得:原式=
+(z+27)2=0,∴x-4=0,y+8=0,z+27=0,∴x=4,y=-8,z=-27,将三个数代入原式得:原式=![]() +
+![]() -
-![]() =2-2+3=3;(3),令a2-3=0或1,解得:a=±
=2-2+3=3;(3),令a2-3=0或1,解得:a=±![]() 或a=±2.
或a=±2.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10). 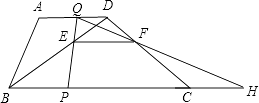
(1)当t为何值时,四边形PCDQ为平行四边形?
(2)在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)求A,B两种商品每件各是多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) (2![]() -3
-3![]() )÷
)÷![]() ; (2) (
; (2) (![]() -
-![]() )2+2
)2+2![]() ×
×![]() ;
;
(3) ![]() ; (4) (
; (4) (![]() -2
-2![]() )×
)×![]() -4
-4![]() ;
;
(5)(![]() -1)(
-1)(![]() +1)-(-
+1)-(-![]() )-2+|1-
)-2+|1-![]() |-(π-2)0+
|-(π-2)0+![]() ;
;
(6)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:设a+b
)2.善于思考的小明进行了以下探索:设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n均为整数),则有a+b
)2(其中a,b,m,n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.请你仿照小明的方法解决下列问题:
的式子化为平方式的方法.请你仿照小明的方法解决下列问题:
(1)当a,b,m,n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分别表示a,b,得a=______________,b=________;
)2,用含m,n的式子分别表示a,b,得a=______________,b=________;
(2)利用所探索的结论,找一组正整数a,b,m,n填空:
________+________![]() =(________+________
=(________+________![]() )2;
)2;
(3)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n均为正整数,求a的值.
)2,且a,m,n均为正整数,求a的值.
(4)试化简![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次知识竞赛共有20道题,每一题答对得5分,答错或不答都扣3分.
(1)小明考了68分,那么小明答对了多少问题?
(2)小亮获得二等奖(70分~90分),请你算算小亮答对了几道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,四块阴影部分的面积分别为S1、S2、S3、S4.则S1+S2+S3+S4等于( )
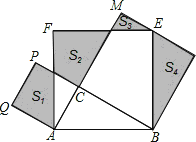
A.14 B.16 C.18 D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com