
【题目】某公司销售的一种时令商品每件成本为20元,经过市场调查分析,5月份的日销售件数为:![]() (其中t为天数),并且前15天,每天的价格
(其中t为天数),并且前15天,每天的价格![]() (元/件)与时间t(天)的函数关系式为
(元/件)与时间t(天)的函数关系式为![]() (
(![]() ,且t为整数),第16天到月底每天的价格
,且t为整数),第16天到月底每天的价格![]() (元/件)与时间t(天)的函数关系式为
(元/件)与时间t(天)的函数关系式为![]() (
(![]() ,且t为整数),根据以上信息,解答下列问题:
,且t为整数),根据以上信息,解答下列问题:
(1)5月份第10天的销售件数为________件,销售利润为________元;
(2)请通过计算预测5月份中哪一天的日销售利润w最大,最大日销售利润是多少?
(3)在实际销售的前15天中,该公司决定每销售一件商品就捐赠m元利润![]() 给希望工程.公司通过销售记录发现,前15天中,每天扣除捐赠后的日销售利润w随t的增大而增大,求m的取值范围.
给希望工程.公司通过销售记录发现,前15天中,每天扣除捐赠后的日销售利润w随t的增大而增大,求m的取值范围.
参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是 .
.
【答案】(1)76,570;(2)预测5月份中第16天的日销售利润最大,最大日销售利润是1792元;(3)![]()
【解析】
(1)76,570;
【解法提示】当![]() 时,销售件数为
时,销售件数为![]() (件),销售价格
(件),销售价格![]() (元/件),∴销售利润为
(元/件),∴销售利润为![]() 元.
元.
(2)①当![]() 时,
时,
![]()
![]()
![]() .
.
∵![]() ,∴对称轴
,∴对称轴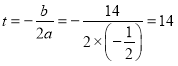 ,
,
又∵![]() ,
,
∴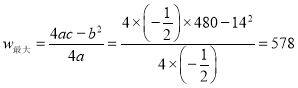 ,
,
∴当![]() 时,w有最大值578元;
时,w有最大值578元;
②当![]() 时,
时,![]()
![]()
![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴当![]() 时,w随t的增大而减小,
时,w随t的增大而减小,
∴当![]() 时,w有最大值为
时,w有最大值为![]() 元.
元.
∵![]() ,
,
∴第16天时,销售利润最大,为1792元.
答:预测5月份中第16天的日销售利润最大,最大日销售利润是1792元;
(3)![]() ,对称轴为
,对称轴为![]() ,
,
∵![]() ,∴只有当
,∴只有当![]() 时,w随t的增大而增大,
时,w随t的增大而增大,
又每天扣除捐赠后的日销售利润w随时间t的增大而增大,
∴![]() ,解得
,解得![]() ,
,
即![]() 时,w随t的增大而增大,
时,w随t的增大而增大,
又∵![]() ,∴
,∴![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在2019年某中学举行的冬季阳径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种成本为每台20元的台灯,规定销售单价不低于成本价,又不高于每台32元.销售中平均每月销售量y(台)与销售单价x(元)的关系可以近似地看做一次函数,如下表所示:
x | 22 | 24 | 26 | 28 |
y | 90 | 80 | 70 | 60 |
(1)请直接写出y与x之间的函数关系式;
(2)为了实现平均每月375元的台灯销售利润,这种台灯的售价应定为多少?这时每月应购进台灯多少个?
(3)设超市每月台灯销售利润为ω(元),求ω与x之间的函数关系式,当x取何值时,ω的值最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育器材专卖柜经销A、B两种器材,A种器材每件进价350元,售价480元;B种器材每件进价200元,售价300元.
(1)该专卖柜计划用8000元去购进A、B两种器材若干件.
①若购进A种器材x件,B种器材y件,所获利润w元,请写出w与x之间满足的函数关系式;
②怎样购进才能使专卖柜经销这两种器材所获利润最大(其中A种器材不少于7件)?
(2)在“五·一”期间,该专卖柜对A、B两种器材进行如下优惠促销活动:
一次性购物总金额 | 优惠措施 |
不超过3000元 | 不优惠 |
超过3000元不超过4000元 | 售价打八折 |
超过4000元 | 售价打七折 |
促销活动期间:甲学校去该专卖柜购买A种器材付款2688元;乙学校去该专卖柜购买B种器材付款2100元,求丙学校决定一次性购买甲学校和乙学校购买的同样多的器材需付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
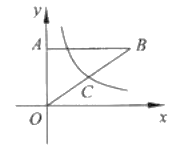
【题目】如图,在平面直角坐标系中,![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在第一象限,函数
在第一象限,函数![]() 的图象与边
的图象与边![]() 交于点
交于点![]() ,并且点
,并且点![]() 为边
为边![]() 的中点.若
的中点.若![]() 的面积为12,则
的面积为12,则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知:函数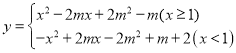 .
.
(1)当![]() 时,
时,
①求![]() 随
随![]() 增大而增大时,
增大而增大时,![]() 的取值范围;
的取值范围;
②当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
③当![]() 时,设
时,设![]() 的最大值与最小值之差为
的最大值与最小值之差为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() ,连结
,连结![]() .当此函数的图象与线段
.当此函数的图象与线段![]() 只有两个公共点时,直接写出
只有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
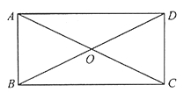
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线![]() 与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
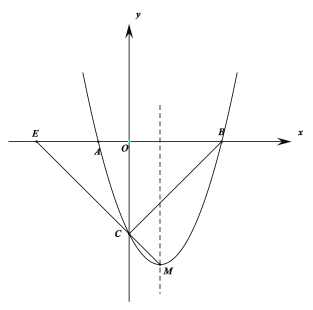
(1)求点C及顶点M的坐标.
(2)若点N是第四象限内抛物线上的一个动点,连接![]() 求
求![]() 面积的最大值及此时点N的坐标.
面积的最大值及此时点N的坐标.
(3)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.
(4)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P、E、O为顶点的三角形与![]() 相似.若存在,求出点P的坐标;若不存在,请说明理由.
相似.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com