
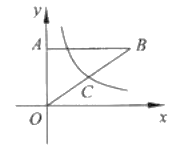
【题目】如图,在平面直角坐标系中,![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在第一象限,函数
在第一象限,函数![]() 的图象与边
的图象与边![]() 交于点
交于点![]() ,并且点
,并且点![]() 为边
为边![]() 的中点.若
的中点.若![]() 的面积为12,则
的面积为12,则![]() 的值为______.
的值为______.
【答案】6
【解析】
过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,由此可知![]() ODC∽
ODC∽![]() OEB,CD∥BE,结合
OEB,CD∥BE,结合![]() AOB为直角三角形可得出四边形OEBA为矩形,从而得出“BE=AO,AB=OE”,再由点C为线段OB的中点,即可得出“BE=2CD,OE=2OD”,结合三角形的面积公式以及反比例函数系数k的几何意义即可得出|k|=6,结合反比例函数在第一象限内有图象即可得出结论.
AOB为直角三角形可得出四边形OEBA为矩形,从而得出“BE=AO,AB=OE”,再由点C为线段OB的中点,即可得出“BE=2CD,OE=2OD”,结合三角形的面积公式以及反比例函数系数k的几何意义即可得出|k|=6,结合反比例函数在第一象限内有图象即可得出结论.
解:过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,如图所示.
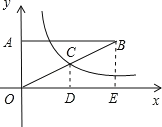
∵CD⊥x轴,BE⊥x轴,
∴![]() ODC∽
ODC∽![]() OEB,CD∥BE.
OEB,CD∥BE.
∵![]() AOB为直角三角形,
AOB为直角三角形,
∴∠OAB=90°=∠AOE,
∴AB∥OE,
∴四边形OEBA为矩形,
∴BE=AO,AB=OE.
又∵点C为线段OB的中点,
∴BE=2CD,OE=2OD.
∵S△AOB=![]() AOAB
AOAB
=![]() BEOE
BEOE
=![]() (2CD)(2OD)
(2CD)(2OD)
=4S△OCD
=12,
∴S△OCD=3=![]() |k|,
|k|,
解得:|k|=6.
∵反比例函数图象有一部分在第一象限内,
∴k=6.
故答案为:6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某网店正在热销一款电子产品,其成本为10元/件,销售中发现,该商品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的关系:
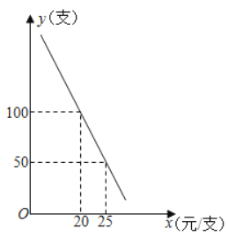
(1)请求出y与x之间的函数关系式;
(2)该款电子产品的销售单价为多少元时,每天销售利润最大?最大利润是多少元;
(3)由于武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出300元捐赠给武汉,为了保证捐款后每天剩余利润不低于450元,如何确定该款电子产品的销售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年3月12日植树节,某校组织七、八、九三个年级的部分学生参加植树活动,活动结束后,领队的老师统计各年级学生及植树情况得到如下3条信息:根据信息,解答下列问题:
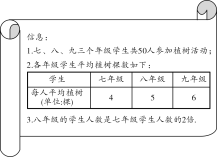
设七年级有x名学生参加植树活动,三个年级学生共植树y棵.
(1)求y关于x的函数解析式;
(2)若各年级学生共植树256棵,七年级有多少名学生人参加植树活动;
(3)若九年级学生植树数量占总数的百分比不超过![]() ,求所有学生植树数量的最大值.
,求所有学生植树数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售的一种时令商品每件成本为20元,经过市场调查分析,5月份的日销售件数为:![]() (其中t为天数),并且前15天,每天的价格
(其中t为天数),并且前15天,每天的价格![]() (元/件)与时间t(天)的函数关系式为
(元/件)与时间t(天)的函数关系式为![]() (
(![]() ,且t为整数),第16天到月底每天的价格
,且t为整数),第16天到月底每天的价格![]() (元/件)与时间t(天)的函数关系式为
(元/件)与时间t(天)的函数关系式为![]() (
(![]() ,且t为整数),根据以上信息,解答下列问题:
,且t为整数),根据以上信息,解答下列问题:
(1)5月份第10天的销售件数为________件,销售利润为________元;
(2)请通过计算预测5月份中哪一天的日销售利润w最大,最大日销售利润是多少?
(3)在实际销售的前15天中,该公司决定每销售一件商品就捐赠m元利润![]() 给希望工程.公司通过销售记录发现,前15天中,每天扣除捐赠后的日销售利润w随t的增大而增大,求m的取值范围.
给希望工程.公司通过销售记录发现,前15天中,每天扣除捐赠后的日销售利润w随t的增大而增大,求m的取值范围.
参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上,![]() 连接
连接![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.
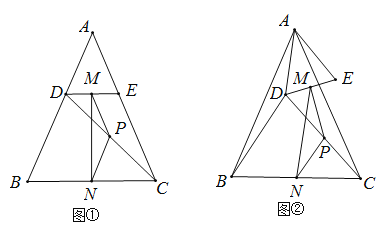
[观察猜想]图①,线段![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() _____
_____![]() ;
;
[探究证明]把![]() 绕点
绕点![]() 逆时针方向旋转到图②的位置,连结
逆时针方向旋转到图②的位置,连结![]() ,上述猜想的结论是否成立,请说明理由.
,上述猜想的结论是否成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①表示的是某商场2012年前四个月中两个月的商品销售额的情况,图②表示的是商场家电部各月销售额占商场当月销售总额的百分比情况,观察图①、图②解答下列问题:
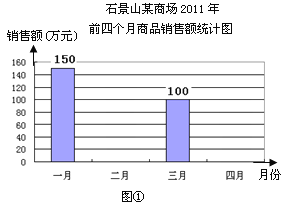
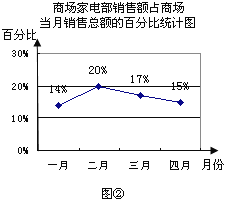
(1)商场前四个月财务结算显示四月份商场的商品销售额比一月份下降了20%,请你求出商场四月份的销售额;
(2)若商场前四个月的商品销售总额一共是500万元,请你根据这一信息将图①中的统计图补充完整;
(3)小明观察图②后认为,商场家电部四月份的销售额比三月份减少了,你同意他的看法吗?请你说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,直线l1分别交x轴和y轴于点A(﹣3,0),B(0,3).
(1)如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长;
(2)如图2,已知直线l2:y=3x﹣3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心,2![]() 为半径画圆.
为半径画圆.
①当点Q与点C重合时,求证:直线l1与⊙Q相切;
②设⊙Q与直线l1相交于M,N两点,连结QM,QN.问:是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,动点
,动点![]() ,
,![]() 分别从
分别从![]() 点,
点,![]() 点同时以每秒1个单位长度的速度出发,且分别在边
点同时以每秒1个单位长度的速度出发,且分别在边![]() 上沿
上沿![]() ,
,![]() 的方向运动,当点
的方向运动,当点![]() 运动到点
运动到点![]() 时,
时,![]() 两点同时停止运动,设点
两点同时停止运动,设点![]() 运动的时间为
运动的时间为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与边
与边![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
(1)如图2,当![]() 时,延长
时,延长![]() 交边
交边![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)在(1)的条件下,试探究线段![]() 三者之间的等量关系,并加以证明;
三者之间的等量关系,并加以证明;
(3)如图3,当![]() 时,延长
时,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 平分
平分![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com