
【题目】已知在平面直角坐标系xOy中,直线l1分别交x轴和y轴于点A(﹣3,0),B(0,3).
(1)如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长;
(2)如图2,已知直线l2:y=3x﹣3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心,2![]() 为半径画圆.
为半径画圆.
①当点Q与点C重合时,求证:直线l1与⊙Q相切;
②设⊙Q与直线l1相交于M,N两点,连结QM,QN.问:是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标;若不存在,请说明理由.

【答案】(1)3![]() ;(2)①见解析,②存在,Q1(3–
;(2)①见解析,②存在,Q1(3–![]() ,6–3
,6–3![]() )和Q2(3+
)和Q2(3+![]() ,6+3
,6+3![]() )
)
【解析】
(1)证明△ABC为等腰直角三角形,则⊙P的直径长=BC=AB,即可求解;
(2)过点C作CE⊥AB于点E,证明CE=ACsin45°=4×![]() =2
=2![]() =圆的半径,即可求解;
=圆的半径,即可求解;
(3)分点M、N在两条直线交点的下方、点M、N在两条直线交点的上方两种情况,分别求解即可.
证明:(1)如图1,连接BC,
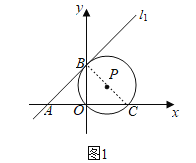
∵∠BOC=90°,∴点P在BC上,
∵⊙P与直线l1相切于点B,
∴∠ABC=90°,而OA=OB,
∴△ABC为等腰直角三角形,
则⊙P的直径长=BC=AB=3![]() ;
;
(2)①过点C作CE⊥AB于点E,如图2.
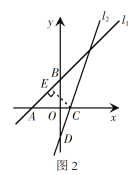
将y=0代入y=3x–3,得x=1,
∴点C的坐标为(1,0).∴AC=4,
∵∠CAE=45°,∴CE=![]() AC=2
AC=2![]() ,
,
∵点Q与点C重合,又⊙Q的半径为2![]() ,
,
直线l1与⊙Q相切.
②假设存在这样的点Q,使得△QMN是等腰直角三角形,
∵直线l1经过点A(–3,0),B(0,3),
∴l1的函数解析式为y=x+3.
记直线l2与l1的交点为F,
情况一:
当点Q在线段CF上时,由题意,得∠MNQ=45°,
延长NQ交x轴于点G,如图3,
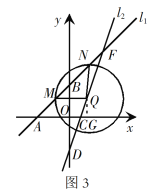
∵∠BAO=45°,
∴∠NGA=180°–45°–45°=90°,
即NG⊥x轴,∴点Q与N有相同的横坐标,
设Q(m,3m–3),则N(m,m+3),
∴QN=m+3–(3m–3),
∵⊙Q的半径为2![]() ,
,
∴m+3–(3m–3)=2![]() ,解得m=3–
,解得m=3–![]() ,
,
3m–3=6–3![]() ,
,
∴Q的坐标为(3–![]() ,6–3
,6–3![]() ).
).
情况二:
当点Q在线段CF的延长线上时,如图4,
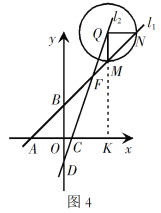
同理可得m=3+![]() ,
,
Q的坐标为(3+![]() ,6+3
,6+3![]() ).
).
∴存在这样的点Q1(3–![]() ,6–3
,6–3![]() )和Q2(3+
)和Q2(3+![]() ,6+3
,6+3![]() ),使得△QMN是等腰直角三角形.
),使得△QMN是等腰直角三角形.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】小明在一次打篮球时,篮球传出后的运动路线为如图所示的抛物线,以小明所站立的位置为原点O建立平面直角坐标系,篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=-![]() x2+x+c.
x2+x+c.
(1)求y与x之间的函数表达式;
(2)球在运动的过程中离地面的最大高度;
(3)小亮手举过头顶,跳起后的最大高度为BC=2.5m,若小亮要在篮球下落过程中接到球,求小亮离小明的最短距离OB.

查看答案和解析>>
科目:初中数学 来源: 题型:
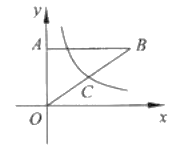
【题目】如图,在平面直角坐标系中,![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在第一象限,函数
在第一象限,函数![]() 的图象与边
的图象与边![]() 交于点
交于点![]() ,并且点
,并且点![]() 为边
为边![]() 的中点.若
的中点.若![]() 的面积为12,则
的面积为12,则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚质地均匀的硬币正面朝上的概率为![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.连续抛一枚均匀硬币2次必有1次正面朝上
B.连续抛一枚均匀硬币5次,正面都朝上是不可能事件
C.大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
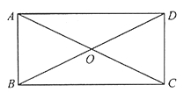
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年1月份,某药店计划购进一批甲、乙两种型号的口罩,已知一袋甲种口罩的进价与一袋乙种口罩的进价和为40元,用90元购进甲种口罩的袋数与用150元购进乙种口罩的袋数相同.求每袋甲种、乙种口罩的进价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
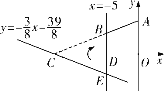
【题目】(2017河北24题10分)如图,直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() ,
,![]() ,点
,点![]() ,
,![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
(1)求点![]() ,
,![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,而
的位置,而![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com