
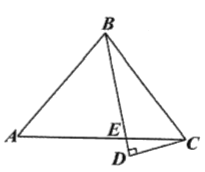
【题目】如图,![]() 中,点
中,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() ,
,![]() 垂直于
垂直于![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() ,则边
,则边![]() 的长为_____.
的长为_____.
【答案】![]()
【解析】
如图,延长BD到点G,使DG=BD,连接CG,则由线段垂直平分线的性质可得CB=CG,在EG上截取EF=EC,连接CF,则∠EFC=∠ECF,∠G=∠CBE,根据等腰三角形的性质和三角形的内角和定理可得∠EFC=∠A=2∠CBE,再根据三角形的外角性质和等腰三角形的判定可得FC=FG,设CE=EF=x,则可根据线段间的和差关系求出DF的长,进而可求出FC的长,然后根据勾股定理即可求出CD的长,再一次运用勾股定理即可求出答案.
解:如图,延长BD到点G,使DG=BD,连接CG,则CB=CG,在EG上截取EF=EC,连接CF,则∠EFC=∠ECF,∠G=∠CBE,
∵EA=EB,∴∠A=∠EBA,
∵∠AEB=∠CEF,
∴∠EFC=∠A=2∠CBE=2∠G,
∵∠EFC=∠G+∠FCG,
∴∠G=∠FCG,
∴FC=FG,
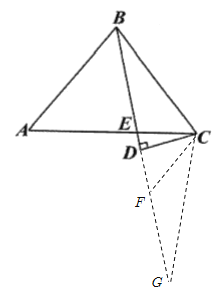
设CE=EF=x,则AE=BE=11-x,
∴DE=8-(11-x)=x-3,
∴DF=x-(x-3)=3,
∵DG=DB=8,
∴FG=5,∴CF=5,
在Rt△CDF中,根据勾股定理,得![]() ,
,
∴![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
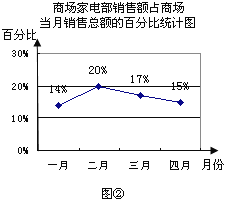
【题目】图①表示的是某商场2012年前四个月中两个月的商品销售额的情况,图②表示的是商场家电部各月销售额占商场当月销售总额的百分比情况,观察图①、图②解答下列问题:
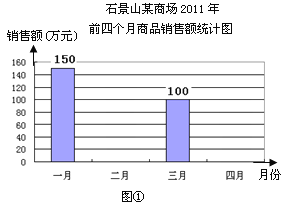
(1)商场前四个月财务结算显示四月份商场的商品销售额比一月份下降了20%,请你求出商场四月份的销售额;
(2)若商场前四个月的商品销售总额一共是500万元,请你根据这一信息将图①中的统计图补充完整;
(3)小明观察图②后认为,商场家电部四月份的销售额比三月份减少了,你同意他的看法吗?请你说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,直线l1分别交x轴和y轴于点A(﹣3,0),B(0,3).
(1)如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长;
(2)如图2,已知直线l2:y=3x﹣3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心,2![]() 为半径画圆.
为半径画圆.
①当点Q与点C重合时,求证:直线l1与⊙Q相切;
②设⊙Q与直线l1相交于M,N两点,连结QM,QN.问:是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第33个国际禁毒日到来之际,贵阳市策划了以“健康人生绿色无毒”为主题的禁毒宣传月活动,某班开展了此项活动的知识竞赛.学习委员为班级购买奖品后与生活委员对话如下:

(1)请用方程的知识帮助学习委员计算一下,为什么说学习委员搞错了;
(2)学习委员连忙拿出发票,发现的确错了,因为他还买了一本笔记本,但笔记本的单价已模糊不清,只能辨认出单价是小于10元的整数,那么笔记本的单价可能是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区统计了有扶贫任务的人员一个月下乡扶贫的天数(为整数),并制成了如下尚不完整的表格与条形统计图(如图).
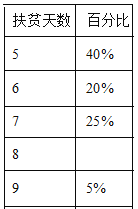
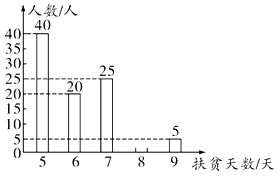
(1)有扶贫任务的人员的总人数是__________,并补全条形统计图;
(2)上级部门随机抽查1名扶贫人员,检查其工作情况,求抽查到的扶贫人员的扶贫天数大于7天的概率;
(3)若统计时漏掉1名扶贫人员,现将他的下乡天数和原统计的下乡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名扶贫人员下乡的天数最少是多少天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,动点
,动点![]() ,
,![]() 分别从
分别从![]() 点,
点,![]() 点同时以每秒1个单位长度的速度出发,且分别在边
点同时以每秒1个单位长度的速度出发,且分别在边![]() 上沿
上沿![]() ,
,![]() 的方向运动,当点
的方向运动,当点![]() 运动到点
运动到点![]() 时,
时,![]() 两点同时停止运动,设点
两点同时停止运动,设点![]() 运动的时间为
运动的时间为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与边
与边![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
(1)如图2,当![]() 时,延长
时,延长![]() 交边
交边![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)在(1)的条件下,试探究线段![]() 三者之间的等量关系,并加以证明;
三者之间的等量关系,并加以证明;
(3)如图3,当![]() 时,延长
时,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 平分
平分![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com