
分析 根据题意画出图形,写出已知,求证,根据全等三角形的判定求出Rt△AMB≌Rt△DNE,根据全等三角形的性质得出∠A=∠D,再根据SAS推出即可.
解答 已知:如图,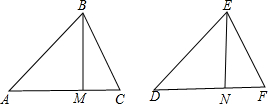
△ABC和△DEF中,AC=DF,AB=DE,BM⊥AC于M,EN⊥DF于N,BM=EN,
求证:△ABC≌△DEF,
证明:∵BM⊥AC,EN⊥DF,
∴∠AMB=∠DNE=90°,
在Rt△AMB和Rt△DNE中
$\left\{\begin{array}{l}{AB=DE}\\{BM=EN}\end{array}\right.$
∴Rt△AMB≌Rt△DNE(HL),
∴∠A=∠D,
在△ABC和△DEF中
$\left\{\begin{array}{l}{AB=DE}\\{∠A=∠D}\\{AC=DF}\end{array}\right.$
∴△ABC≌△DEF(SAS).
点评 本题考查了全等三角形的判定定理和性质定理的应用,能熟练地运用全等三角形的判定和性质定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.


 核心素养学练评系列答案
核心素养学练评系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
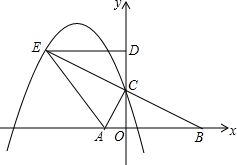 如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.
如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,写出各顶点的坐标.
如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,写出各顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com