
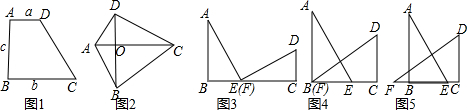
分析 (1)连接AD,由四边形ABCD的面积=△ABE的面积+△FCD的面积+△ADE的面积,得出$\frac{1}{2}$(a+b)2=$\frac{1}{2}$ab×2+$\frac{1}{2}$c2,即可得出结论;
(2)连接AD、DE,四边形ABCD的面积=四边形ABED的面积+△DCE的面积,得出$\frac{1}{2}$(a+b)×a=$\frac{1}{2}$c2+$\frac{1}{2}$b(a-b),即可得出结论;
(3)连接AF、AD、DE,设CE=x,则BE=b,FB=a-b-x,由△ABF的面积+四边形ABCD的面积=四边形AFED的面积+△CDE的面积,得出$\frac{1}{2}$a(a-b-x)+$\frac{1}{2}$(a+b)(b+x)=$\frac{1}{2}$c2+$\frac{1}{2}$bx,即可得出结论.
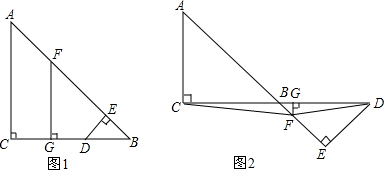
解答 (1)证明:连接AD,如图1所示: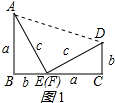
则四边形ABCD是直角梯形,
∴四边形ABCD的面积=$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(a+b)2,
∵四边形ABCD的面积=△ABE的面积+△FCD的面积+△ADE的面积,
即$\frac{1}{2}$(a+b)2=$\frac{1}{2}$ab×2+$\frac{1}{2}$c2,
化简得:(a+b)2=2ab+c2,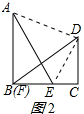
∴a2+b2=c2;
(2)证明:连接AD、DE,如图2所示:
则四边形ABCD的面积=四边形ABED的面积+△DCE的面积,
即$\frac{1}{2}$(a+b)×a=$\frac{1}{2}$c2+$\frac{1}{2}$b(a-b),
化简得:ab+a2=c2+ab-b2,
∴a2+b2=c2;
(3)成立;理由如下: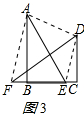
连接AF、AD、DE,如图3所示:
设CE=x,则BE=b,FB=a-b-x,
∵△ABF的面积+四边形ABCD的面积=四边形AFED的面积+△CDE的面积,
∴$\frac{1}{2}$a(a-b-x)+$\frac{1}{2}$(a+b)(b+x)=$\frac{1}{2}$c2+$\frac{1}{2}$bx,
化简得:a2-ab-ax+ab+ax+b2+bx=c2+bx,
∴a2+b2=c2.
点评 本题是四边形综合题目,考查了勾股定理的证明、四边形面积的计算方法、三角形面积的计算等知识;本题综合性强,通过作辅助线,运用面积法证明勾股定理是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数2.4×104精确到十分位 | |
| B. | 将数60340精确到千位是6.0×104 | |
| C. | 按科学记数法表示的6.05×105,其原数是60500 | |
| D. | 近似数8.1750是精确到0.001 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
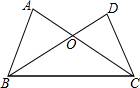 如图,下列条件不能证明△ABC≌△DCB的是( )
如图,下列条件不能证明△ABC≌△DCB的是( )| A. | AB=DC,AC=DB | B. | AB=DC,∠ABC=∠DCB | C. | BO=CO,∠A=∠D | D. | AC=BD,∠A=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com