
 已知函数y=ax2+bx+c的图象如图所示,那么能ax2+bx+c=0的解是( )
已知函数y=ax2+bx+c的图象如图所示,那么能ax2+bx+c=0的解是( )| A. | -3,-1 | B. | -3,0 | C. | -3 | D. | 3 |
科目:初中数学 来源: 题型:解答题
 如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30s | B. | 40s | C. | 50s | D. | 60s |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
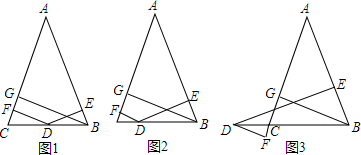
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com