
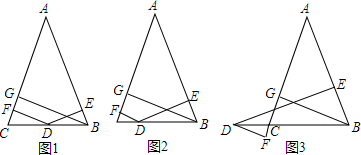
分析 (1)连结AD.根据△ABC的面积=△ABD的面积+△ACD的面积,以及AB=AC,即可得到DE+DF=BG,然后根据等腰直角三角形的性质即可得到结论;
(2)连结AD.根据△ABC的面积=△ABD的面积+△ACD的面积,以及AB=AC,即可得到DE+DF=BG;
(3)连结AD.根据△ABC的面积=△ABD的面积-△ACD的面积,以及AB=AC,即可得到DE-DF=BG.
解答 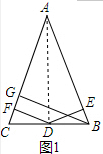 解:如图1,连结AD.
解:如图1,连结AD.
则△ABC的面积=△ABD的面积+△ACD的面积,即$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$AC•BG,
∵AB=AC,
∴DE+DF=BG,
∵D是BC边上的中点,∴AD平分∠BAC,
∴DE=DF=3,
∴BG=6,
∵∠A=45°,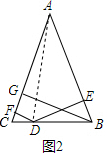
∴△AGB是等腰直角三角形,
∴AB=$\sqrt{2}$BG=6$\sqrt{2}$,
∴AC=6$\sqrt{2}$;
(2)证明:如图2,连结AD.
则△ABC的面积=△ABD的面积+△ACD的面积,
即$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$AC•BG,
∵AB=AC,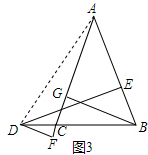
∴DE+DF=BG;
(3)DE-DF=BG,
证明:如图3,连接AD,则△ABC的面积=△ABD的面积-△ACD的面积,
即$\frac{1}{2}$AB•DE-$\frac{1}{2}$AC•DF=$\frac{1}{2}$AC•BG,
∵AB=AC,
∴DE-DF=BG.
点评 本题考查了三角形的面积和等腰三角形的性质,本题关键是根据三角形面积的两种不同表示方法求解.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
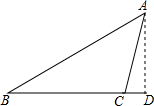 如图,在△ABC中,∠B=30°,BC=40cm,过点A作AD⊥BC,垂足为D,∠ACD=75°.
如图,在△ABC中,∠B=30°,BC=40cm,过点A作AD⊥BC,垂足为D,∠ACD=75°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=110°,α的度数是( )
如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=110°,α的度数是( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1的函数表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
如图,直线l1的函数表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
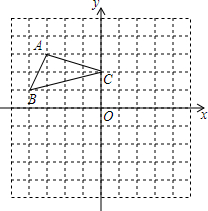 方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若$\frac{{S}_{△BDE}}{{S}_{△DEC}}$=$\frac{1}{3}$,则$\frac{{S}_{△BDE}}{{S}_{△ACD}}$的值等于( )
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若$\frac{{S}_{△BDE}}{{S}_{△DEC}}$=$\frac{1}{3}$,则$\frac{{S}_{△BDE}}{{S}_{△ACD}}$的值等于( )| A. | 1:5 | B. | 1:9 | C. | 1:12 | D. | 1:16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com