
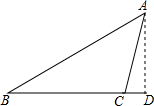
 如图,在△ABC中,∠B=30°,BC=40cm,过点A作AD⊥BC,垂足为D,∠ACD=75°.
如图,在△ABC中,∠B=30°,BC=40cm,过点A作AD⊥BC,垂足为D,∠ACD=75°.分析 (1)过C点作CE⊥AB于E,如图,在Rt△BCD中,利用含30°的直角三角形三边的关系易得CH=$\frac{1}{2}$BC=20;
(2)在Rt△BCD中利用含30°的直角三角形三边的关系易得CH=20,BH=$\sqrt{3}$CH=20$\sqrt{3}$,再利用三角形外角性质计算出∠BAC=45°,则△ACH为等腰直角三角形,所以AH=CH=20,然后利用面积法求AD.
解答 解:(1)过C点作CE⊥AB于E,如图,
在Rt△BCD中,∵∠B=30°,
∴CH=$\frac{1}{2}$BC=$\frac{1}{2}$×40=20,
即点C到AB的距离为20cm;
(2)在Rt△BCD中,∵∠B=30°,
∴CH=20,BH=$\sqrt{3}$CH=20$\sqrt{3}$,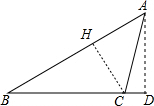
∵∠ACD=∠B+∠BAC,
∴∠BAC=75°-30°=45°,
∴△ACH为等腰直角三角形,
∴AH=CH=20,
∴AB=20$\sqrt{3}$+20,
∵$\frac{1}{2}$AD•BC=$\frac{1}{2}$CH•AB,
∴AD=$\frac{20×(20\sqrt{3}+20)}{40}$=10$\sqrt{3}$+10.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是利用面积法求AD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
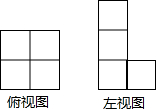 如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,则组成这个几何体的小正方体的个数是( )
如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,则组成这个几何体的小正方体的个数是( )| A. | 5或6或7 | B. | 6或7 | C. | 7或8 | D. | 6或7或8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com