
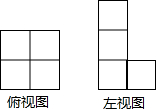
 如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,则组成这个几何体的小正方体的个数是( )
如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,则组成这个几何体的小正方体的个数是( )| A. | 5或6或7 | B. | 6或7 | C. | 7或8 | D. | 6或7或8 |
分析 首先根据几何体的左视图,可得这个几何体共有3层;然后从俯视图中可以看出最底层小正方体的个数及形状;最后从左视图判断出第二层、第三层的个数,进而求出组成这个几何体的小正方体的个数是多少即可.
解答 解:根据几何体的左视图,可得这个几何体共有3层,
从俯视图可以可以看出最底层的个数是4个,
(1)当第一层有1个小正方体,第二层有1个小正方体时,
组成这个几何体的小正方体的个数是:
1+1+4=6(个);
(2)当第一层有1个小正方体,第二层有2个小正方体时,
或当第一层有2个小正方体,第二层有1个小正方体时,
组成这个几何体的小正方体的个数是:
1+2+4=7(个);
(3)当第一层有2个小正方体,第二层有2个小正方体时,
组成这个几何体的小正方体的个数是:
2+2+4=8(个).
综上,可得
组成这个几何体的小正方体的个数是6或7或8.
故选:D.
点评 此题主要考查了由三视图判断几何体,考查了空间想象能力,要熟练掌握,解答此题的关键是要明确:由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.


科目:初中数学 来源: 题型:解答题
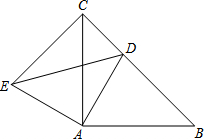 已知:如图,等腰△ABC,AB=AC,点D为△ABC的BC边上一点,连接AD,将线段AD旋转至AE,使得∠DAE=∠BAC,连接CE.
已知:如图,等腰△ABC,AB=AC,点D为△ABC的BC边上一点,连接AD,将线段AD旋转至AE,使得∠DAE=∠BAC,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
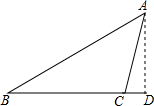 如图,在△ABC中,∠B=30°,BC=40cm,过点A作AD⊥BC,垂足为D,∠ACD=75°.
如图,在△ABC中,∠B=30°,BC=40cm,过点A作AD⊥BC,垂足为D,∠ACD=75°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 单价(元/千克) | 质量(千克) | 销售额(元) | |
| 加工前 | x | 30 | 30x |
| 加工后 | (1+20%)x | 30×90% | (1+20%)x×(30×90%) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=110°,α的度数是( )
如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=110°,α的度数是( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1的函数表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
如图,直线l1的函数表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com