
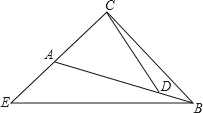
【题目】如图,在△BCE中,∠ACB=∠CAB+30°=∠ABC+60°,在边AB上取点D,在CA的延长线上取点E,使ACCE+ABBD=BC2
求证:(1)∠CEB>∠ABC;
(2)BE=2CD.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)延长CE到F,使EF=2BD,由∠ACB=∠CAB+30°=∠ABC+60°,可得∠ACB=90°,又ACCE+ABBD=BC2,等量代换可得AC(CE+2BD)=BC2,即![]() ,则△ABC∽△BFC,∠ABC=∠F,根据三角形外角的性质,即可证得;(2)∠F=30°,则BF=2BC,易证△EFB∽△DBC,即可证得BE=2CD.
,则△ABC∽△BFC,∠ABC=∠F,根据三角形外角的性质,即可证得;(2)∠F=30°,则BF=2BC,易证△EFB∽△DBC,即可证得BE=2CD.
证明:(1)延长CE到F,使EF=2BD,
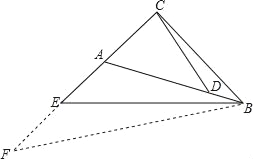
∵在△BCE中,∠ACB=∠CAB+30°=∠ABC+60°,
∴∠ACB=90°,∠ABC=30°,∠CAB=60°,
∴AB=2AC,
∵ACCE+ABBD=BC2,
∴AC(CE+2BD)=BC2,
∴AC×CF=BC2,
即![]() ,
,
∴△ABC∽△BFC,
∴∠ABC=∠F=30°,
∵∠CEB>∠F,
∴∠CEB>∠ABC;
(2)∵∠F=30°,∠FCB=90°,
∴FB=2BC,又∠F=∠CBD,EF=2BD,
∴△EFB∽△DBC,
∴![]() ,
,
∴BE=2CD.


科目:初中数学 来源: 题型:
【题目】如图,在△BAC中,∠B和∠C的平分线相交于点F,过点F作DE∥BC交AB于点D,交AC于点E,若BD=5,CE=4,则线段DE的长为( )
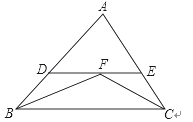
A. 9 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
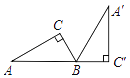
【题目】如图,Rt△A'BC'是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C'在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则Rt△ABC旋转到Rt△A'BC'所扫过的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下列结论:①AC平分∠PAD;②∠APO=∠DCO;③△OPC是等边三角形;④AC=AO+AP;其中正确的序号是( )
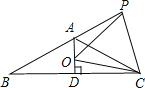
A.①③④B.②③C.①②④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,AG平分∠BAC交BD于G,DE⊥AG于点H.下列结论:①AD=2AE:②FD=AG;③CF=CD:④四边形FGEA是菱形;⑤OF=![]() BE,正确的有( )
BE,正确的有( )
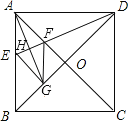
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天晚上,小丽帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),在清洗过程中,突然停电了,小丽只好摸黑清洗(在摸黑清洗中,能分清杯盖与茶杯)
(1)小丽摸黑清洗过程中,在三个茶杯中他随手拿起两个,则这两个都属于有杯盖的茶杯的概率是多少?
(2)小丽摸黑清洗完茶杯和杯盖后,只好把杯盖与茶杯随机地搭配在一起,则花色搭配完全正确的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用指定方法解下列一元二次方程.
(1)x2﹣36=0(直接开平方法)
(2)x2﹣4x=2(配方法)
(3)2x2﹣5x+1=0(公式法)
(4)(x+1)2+8(x+1)+16=0(因式分解法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com