
【题目】一天晚上,小丽帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),在清洗过程中,突然停电了,小丽只好摸黑清洗(在摸黑清洗中,能分清杯盖与茶杯)
(1)小丽摸黑清洗过程中,在三个茶杯中他随手拿起两个,则这两个都属于有杯盖的茶杯的概率是多少?
(2)小丽摸黑清洗完茶杯和杯盖后,只好把杯盖与茶杯随机地搭配在一起,则花色搭配完全正确的概率是多少?

科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,4a),B(3a,0),△AOB的面积是150.
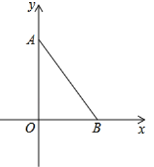
(1)求点A的坐标;
(2)点P是射线AB上的一点,点P的横坐标为t,连接PO,若△PBO的面积为S,试用含有t的式子表示S.
(3)在(2)的条件下,若点P在第一象限内,且S△PBO=126,过P作PE⊥AB,交y轴于点D,交x轴于点E,且OB=OD,连接AE,M为AE上一点,连接OM交PE于点N,若∠EMN+∠ABE=180°,求点N的坐标.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
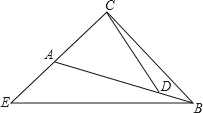
【题目】如图,在△BCE中,∠ACB=∠CAB+30°=∠ABC+60°,在边AB上取点D,在CA的延长线上取点E,使ACCE+ABBD=BC2
求证:(1)∠CEB>∠ABC;
(2)BE=2CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )

A. 36 B. 12 C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
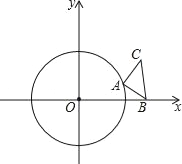
【题目】如图,⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(![]() ,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
(1)当点A在x轴的正半轴上时,直接写出点C的坐标;
(2)当点A运动到x轴的负半轴上时,试判断直线BC与⊙O位置关系,并说明理由;
(3)设点A的横坐标为x,△ABC的面积为S,求S与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点E、F、G分别为边AB、BC、CD的中点,若△EFG的面积为4,则四边形ABCD的面积为( )
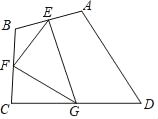
A. 8 B. 12 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线![]() 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由。
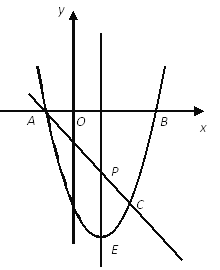
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com