
【题目】如图,已知CB//OA,∠C=∠A=104°,点E,F在BC上,OE平分∠COF,OB平分∠AOF
(1)求证:OC//AB;
(2)求∠EOB的度数;
(3)若平行移动AB,在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,请说明理由.

【答案】(1)见解析;(2)38°;(3)存在,57°
【解析】
(1)先根据两直线平行,同旁内角互补可知:∠C +∠COA =180°,再根据等角代换可得:∠A +∠COA =180°,然后根据平行线的判定定理可得OC∥AB;
(2)根据两直线平行,同旁内角互补求出∠COA,再根据角平分线的定义求出∠EOB=![]() ∠COA,代入数据即可;
∠COA,代入数据即可;
(3)先根据三角形内角和定理求出∠COE=∠BOA,从而得到OE、OF、OB是∠COA的四等分线,再利用三角形内角和定理列式计算即可.
证明:(1)∵ CB∥OA,
∴∠C +∠COA =180° ,
∵∠C=∠A,
∴∠A +∠COA =180°,
∴ OC∥AB;
(2)∵∠C=104°,
∴∠COA=180°-∠C =76° ,
∵ OE平分∠COF,OB平分∠AOF ,
∴∠COE=∠EOF,∠FOB=∠BOA,
∴∠EOB =∠EOF +∠FOB =![]() ∠COF +
∠COF +![]() ∠AOF =
∠AOF =![]() ∠COA =38° ;
∠COA =38° ;
(3)在△COE和△AOB中,
∵∠C =∠A,∠OEC =∠OBA,
∴∠COE =∠BOA ,
∴OE、OF、OB是∠COA的四等分线,
即 ∠COE =∠EOF =∠FOB =∠BOA,
∴∠COE =![]() ∠COA =
∠COA =![]() ×76°=19°,
×76°=19°,
∴∠OEC =180°-∠C -∠COE =180°-104°-19°= 57°,
答:存在某种情况使∠OEC=∠OBA,此时度数为 57°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AD, AC=AE, ∠1=∠2
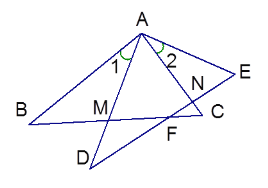
(1)求证:△ABC≌△ADE;
(2)找出图中与∠1 ,∠2相等的角(用图中给出的已知点直接写出结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为直线
为直线![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),分别作
不重合),分别作![]() 和
和![]() 的角平分线,两角平分线所在直线交于点
的角平分线,两角平分线所在直线交于点![]() .
.
(1)若点![]() 在线段
在线段![]() 上,如图1.
上,如图1.
①依题意补全图1;
②求![]() 的度数;
的度数;
(2)当点![]() 在直线
在直线![]() 上运动时,
上运动时,![]() 的度数是否变化?若不变,请说明理由;若变化,画出相应的图形,并直接写出
的度数是否变化?若不变,请说明理由;若变化,画出相应的图形,并直接写出![]() 的度数.
的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,0)和B(0,b)满足![]() ,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置坐标;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在□ABCD内部,AF∥BE,DF∥CE.

(1)求证:△BCE≌△ADF;
(2)设□ABCD的面积为20,求四边形AEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买1张办公桌必须买2把椅子,椅子每把100元,若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元;购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校购买甲乙两种办公桌共40张,且甲种办公桌数量不多于乙种办公桌数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图1,点A,B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小.
小明的思路是:如图2所示,先作点A关于直线l的对称点A′,使点A′,B分别位于直线l的两侧,再连接A′B,根据“两点之间线段最短”可知A′B与直线l的交点P即为所求.
请你参考小明同学的思路,探究并解决下列问题:
(1)如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D.若CP=1,AC=1,PD=2,直接写出AP+BP的值;
(2)将(1)中的条件“AC=1”去掉,换成“BD=4﹣AC”,其它条件不变,直接写出此时AP+BP的值;
(3)请结合图形,求![]() 的最小值.
的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com