
【题目】如图,在△ABC和△ADE中,AB=AD, AC=AE, ∠1=∠2
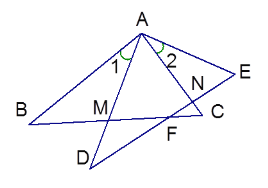
(1)求证:△ABC≌△ADE;
(2)找出图中与∠1 ,∠2相等的角(用图中给出的已知点直接写出结论,不需证明)
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | m=20+ |
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:已知如图,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() .
.

求证:![]() .
.
证明:![]() 平分
平分![]() (__________)
(__________)
![]() (__________)
(__________)
![]() 平分
平分![]() (已知)
(已知)
![]() ____________(角的平分线的定义).
____________(角的平分线的定义).
![]() ___________
___________ ![]() ___________
___________![]() (____________)
(____________)
![]() (___________),
(___________),
![]() ____________(___________)
____________(___________)
![]() (___________).
(___________).
查看答案和解析>>
科目:初中数学 来源: 题型:
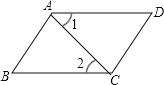
【题目】 根据题意,完成推理填空:如图,AB∥CD,∠1=∠2,试说明∠B=∠D.
解:∵∠1=∠2(已知)
∴ (內错角相等,两直线平行)
∴∠BAD+∠B=180°(两直线平行,同旁内角互补)
∵AB∥CD
∴ + =180°,
∴∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
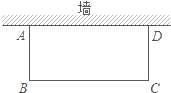
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式.例如: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
含有两个字母![]() ,
, ![]() 的对称式的基本对称式是
的对称式的基本对称式是![]() 和
和![]() ,像
,像![]() ,
, ![]() 等对称式都可以用
等对称式都可以用![]() 和
和![]() 表示,例如:
表示,例如: ![]() .
.
请根据以上材料解决下列问题:
(![]() )式子①
)式子①![]() ,②
,②![]() ,③
,③![]() 中,属于对称式的是__________(填序号).
中,属于对称式的是__________(填序号).
(![]() )已知
)已知![]() .
.
①若![]() ,
, ![]() ,求对称式
,求对称式![]() 的值.
的值.
②若![]() ,直接写出对称式
,直接写出对称式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CB//OA,∠C=∠A=104°,点E,F在BC上,OE平分∠COF,OB平分∠AOF
(1)求证:OC//AB;
(2)求∠EOB的度数;
(3)若平行移动AB,在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com